Next: 2.1.2 Runge の現象 Up: 2.1 補間多項式 Previous: 2.1 補間多項式
![\begin{jproposition}[補間多項式の一意存在]
$[a,b]$ は $\mathbb{R}$\...
...��実係数多項式 $f_n(x)$ が一意的に存在する。
\end{jproposition}](img28.gif)
|
| (3) | 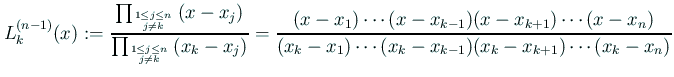 |
| (4) |
| (5) | 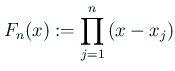 |
| (6) | 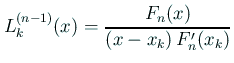 |
| (7) | 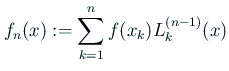 |
以上で存在が示せた。![]() 次多項式の係数
次多項式の係数
![]() (つまり
(つまり
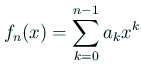 ということ)
を
ということ)
を ![]() ,
, ![]() ,
, ![]() ,
, ![]() での値
での値 ![]() ,
, ![]() ,
,
![]() ,
, ![]() を対応させる写像は、
を対応させる写像は、
![]() から
から
![]() への線型写像である。
上でそれが全射であることが分かった。
線形代数で学ぶ定理によって、それは単射である。
これは
への線型写像である。
上でそれが全射であることが分かった。
線形代数で学ぶ定理によって、それは単射である。
これは ![]() が一意的に定まることを意味している。
が一意的に定まることを意味している。 ![]()
![]()
![]() ,
, ![]() ,
,
![]() を、
を、
![]() ,
, ![]() ,
, ![]() を標本点とする Lagrange 補間係数と呼ぶ。
を標本点とする Lagrange 補間係数と呼ぶ。
上の定理の ![]() を
を ![]() の補間多項式 (interpolating
polynomial) と呼ぶ。
上の議論から分かるように
の補間多項式 (interpolating
polynomial) と呼ぶ。
上の議論から分かるように
| (8) | 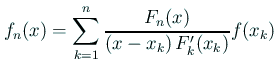 |
(Newtonの補間公式 (Newton 補間多項式, Newton polynomial) というものもあるが、 補間多項式であることには変わりがない。)
桂田 祐史