Next: 4 DE公式 速習 Up: 3.2 での減衰の速い解析関数の積分 に対する台形公式 Previous: 3.2 での減衰の速い解析関数の積分 に対する台形公式
有名な
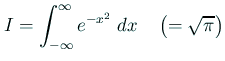
を、適当な
![]() ,
, ![]() ;
; ![]() ,
, ![]() ;
; ![]() ,
, ![]() として実行した
(
として実行した
(![]() は、
は、
![]() の範囲までと考えて定めた。
の範囲までと考えて定めた。![]() のとき、
のとき、
![]() であり、
もう
であり、
もう ![]() を加えても値が変わらない)。
を加えても値が変わらない)。
/*
* example5.c --- 確率積分
* ∞
* I =∫ exp(-x^2)dx = √π
* -∞
* は R 上の解析関数の積分だから、台形則
* ∞
* T_h = h Σ f(n h) (ただし f は被積分関数)
* n=-∞
* あるいは、その打ち切り
* N
* T_{h,N} = h Σ f(n h)
* n=-N
* で非常に精密に計算できるはずである。
*
* コンパイル: cc -o example5 example5.c
*/
#include <stdio.h>
#include <math.h>
typedef double ddfunction(double);
ddfunction f;
double trapezoidal2(ddfunction, double, int);
/* 被積分関数 */
double f(double x)
{
return exp(- x * x);
}
int main(void)
{
int m, N;
double pi, I, h, T;
/* 円周率, 確率積分の真値 */
pi = 4.0 * atan(1.0); I = sqrt(pi);
printf("確率積分の台形則による数値積分\n");
printf(" N h I I-T\n");
h = 1.0;
for (m = 0; m < 3; m++) {
/* [-6,6] で打ち切る */
N = rint(6.0 / h);
T = trapezoidal2(f, h, N);
printf("%2d\t%g\t%20.15f %14e\n", N, h, T, I - T);
h /= 2;
}
return 0;
}
double trapezoidal2(ddfunction f, double h, int N)
{
int j;
double T = 0.0;
for (j = - N; j <= N; j++) T += f(j * h);
T *= h;
return T;
}
|
$ cc -o example5 example5.c $ ./example5 N h I I-T 6 1 1.772453850905516 -1.833539e-04 12 0.5 1.772453850905516 -2.220446e-16 24 0.25 1.772453850905516 -4.440892e-16 |
![\begin{jremark}[$N$ の選び方]
「$N$ は、$-6\le x\le 6$ の範囲ま�...
...nd{screen}を見てもらうと納得出来るだろうか。 \qed
\end{jremark}](img153.gif)
桂田 祐史