Next: 5.4 Eigen ライブラリィを用いた Jordan Up: 5 Laplace 方程式に対する基本解の方法 Previous: 5.2 基本解の方法
天野要は、 §4.3 で述べた 等角写像の求め方と、基本解の方法を組み合わせた、 効率的なアルゴリズムを提唱した ([8])。 それを解説する。
§4.3 で導入した記号を用いる。
![]() の近似
の近似 ![]() を基本解の方法で求めよう。
を基本解の方法で求めよう。
![]() に対して、
に対して、
![]() を
「
を
「![]() を取り囲むように」
を取り囲むように」
![]() から選び、
から選び、
天下りになるが、
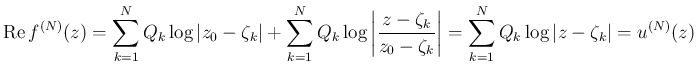
であり、
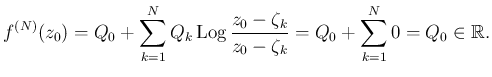
言い換えると
| 天野のアルゴリズム |
桂田 祐史