Next: C. FreeFem++ のマニュアル§3.9 から: Up: FreeFem の紹介 Previous: A. 参考: FreeFem++ で菊地
(ここは書きなおす必要があることが判明したけれど、 しばらくは実行する時間が取れない…書いてあることを信用しないように。)
F. Hecht, O. Pironneau, FreeFem++ a software to solve PDE に分かりやすい解説がある (リンク切れ…と思ったら、マニュアルに入った…と安心していたらなくなった …と思ったら復活した)。 次に掲げるプログラムはそこに載っているもの (ただし変数名を少し書き換えた)である。
| LaplacianEigenvalues.edp |
// LaplacianEigenvlaues.edp
// original: https://doc.freefem.org/models/eigen-value-problems.html
// renamed some variables by mk (2024/8/29)
verbosity=0;
real shift = 20; //value of the shift (near 2 pi^2)
int nev = 20; //number of computed eigenvalues close to shift
// Mesh
mesh Th = square(20, 20, [pi*x, pi*y]);
// Fespace
fespace Vh(Th, P2);
Vh u, v;
// Problem
// AmsB = A - shift B ; // the shifted matrix (A minus shift B)
varf op (u, v)
= int2d(Th)(
dx(u)*dx(v)
+ dy(u)*dy(v)
- shift* u*v
)
+ on(1, 2, 3, 4, u=0)
;
// from the right hand side of -Laplacian u=lambda u
varf b (u, v) = int2d(Th)(u*v); //no boundary condition
matrix AmsB = op(Vh, Vh, solver=Crout, factorize=1); //crout solver because the matrix in not positive
matrix B = b(Vh, Vh, solver=CG, eps=1e-20);
// important remark:
// the boundary condition is make with exact penalization:
// we put 1e30=tgv on the diagonal term of the lock degree of freedom.
// So take Dirichlet boundary condition just on $a$ variational form
// and not on $b$ variational form.
// because we solve $ w=AmsB^-1*B*v $
// Solve
real[int] ev(nev); //to store the nev eigenvalue
Vh[int] eV(nev); //to store the nev eigenvector
int k = EigenValue(AmsB, B, sym=true, sigma=shift, value=ev, vector=eV,
tol=1e-10, maxit=0, ncv=0);
// Display & Plot
for (int i = 0; i < k; i++){
u = eV[i];
real gg = int2d(Th)(dx(u)*dx(u) + dy(u)*dy(u));
real mm = int2d(Th)(u*u) ;
cout << "lambda[" << i << "] = " << ev[i] << ", err= " << int2d(Th)(dx(u)*dx(u) + dy(u)*dy(u) - (ev[i])*u*u) << endl;
plot(eV[i], cmm="Eigenvector "+i+" value ="+ev[i], wait=true, value=true);
}
|
正方形領域
![]() における、
Dirichlet 境界条件下の Laplacian の固有値問題
における、
Dirichlet 境界条件下の Laplacian の固有値問題
| ターミナルで LaplacianEigenvalues.edp を入手して実行 ($ はプロンプトなので入力しない) |
|
$ curl -O https://m-katsurada.sakura.ne.jp/program/fem/LaplacianEigenvalues.edp
$ FreeFem++ LaplacianEigenvalues.edp (領域の三角形分割の後、20個の固有関数の等高線を描くので、 |
![\includegraphics[width=5.5cm]{freefem++/eigenfunc-fig/fig0.eps}](img85.png)
![\includegraphics[width=5.5cm]{freefem++/eigenfunc-fig/fig5.eps}](img86.png)
![\includegraphics[width=5.5cm]{freefem++/eigenfunc-fig/fig19.eps}](img87.png)
なお、8行目の +on(1,2,3,4,u=0) を削除すると、 Dirichlet 境界条件の代わりに、 自然境界条件である Neumann 境界条件となる。
さて、
Dirichlet 境界条件の場合
(5)に、弱形式を導こう。
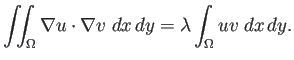
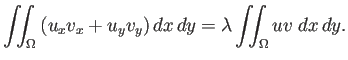
「シフト法で解く」と簡単に書いてあるだけで、詳しいことは書いてない。
次のようなことかと推測する。
一般化固有値に近いと考えられる実数 ![]() を与えたとき、
を与えたとき、
![]() の両辺から
の両辺から
![]() を引くと、
を引くと、
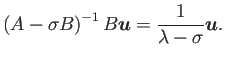
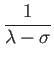 に属する固有ベクトルであることを示す。
ゆえに行列
に属する固有ベクトルであることを示す。
ゆえに行列
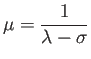 が得られる。
が得られる。
細かいことだが、重要な注意がある。
ここでは square() を用いてメッシュ分割をしているが、
それを用いずに、自分で境界曲線を定義してメッシュ分割をすると、
真の固有値が重複(縮重)する場合であっても、
数値計算で得られる近似固有値は重複(縮重)しない。
これは自動メッシュ分割で得られる三角形分割は、
正方形の二面体群 (合同変換全体のなす群) ![]() の対称性を持たないため、
近似固有値が重複しないためである。
の対称性を持たないため、
近似固有値が重複しないためである。
(2021/1/9加筆) 説明する必要が生じて、昨日久しぶりにここを見て、 抜本的な書き換えはしないけれど (時間がない)、少し補足することに。
桂田 祐史