A. 参考: FreeFem++ で菊地 [1] の Poisson 方程式の例題を解く

菊地 [1] に載っている Poisson 方程式の例題

$$-\Laplacian u=f \mbox{in $\Omega$} ,$$ (2)

$$u=g_1 \mbox{in $\Gamma_1$} ,$$ (3)

$$\frac{\rd u}{\rd n}=g_2 \mbox{in $\Gamma_2$}$$ (4)

(ただし、 $\Omega=(0,1)\times(0,1)$, $\Gamma_1=\{0\}\times[0,1]\cup [0,1]\times\{0\}$, $\Gamma_2=\{1\}\times(0,1]\cup(0,1]\times\{1\}$, $f=1$, $g_1=0$, $g_2=0$) を FreeFem++ を用いて解くにはどうするか。

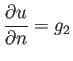例えば次のようなプログラムで解ける。

poisson-kikuchi.edp

// poisson-kikuchi.edp
// https://m-katsurada.sakura.ne.jp/program/fem/poisson-kikuchi.edp
// 菊地文雄, 有限要素法概説, サイエンス社

int Gamma1=1, Gamma2=2;
border Gamma10(t=0,1) { x=0;   y=1-t; label=Gamma1; }
border Gamma11(t=0,1) { x=t;   y=0;   label=Gamma1; }
border Gamma20(t=0,1) { x=1;   y=t;   label=Gamma2; }
border Gamma21(t=0,1) { x=1-t; y=1;   label=Gamma2; }
int m=10;
mesh Th = buildmesh(Gamma10(m)+Gamma11(m)+Gamma20(m)+Gamma21(m));
plot(Th,wait=true,ps="Th.eps");
savemesh(Th,"Th.msh");
fespace Vh(Th,P1);
Vh u,v;
func f=1;
func g1=0;
func g2=0;
solve Poisson(u,v)=
  int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
 -int2d(Th)(f*v)
 -int1d(Th,Gamma2)(g2*v)
 +on(Gamma1,u=g1); // on(Gamma10,Gamma11,u=g1) とも書ける。
plot(u,wait=1,ps="poisson-kikuchi.eps");

//3次元鳥瞰図
//real [int] levels =0.0:0.01:1.0;
//plot(u,dim=3,viso=levels,fill=true,wait=true);

curl -O https://m-katsurada.sakura.ne.jp/program/fem/poisson-kikuchi.edp
FreeFem++ poisson-kikuchi.edp

§2.2 のサンプル・プログラムを叩き台にする。

図 5: poisson-kikuchi.edp -- 要素分割と解の等高線

プログラムで生成される、三角形要素分割のデータを出力できるが、 それは次のようなものである (しばしば、数値実験の三角形要素分割を、 FreeFem++ の出力を拝借している研究者がいる)。

$m=2$ のときの “Th.msh”

9 8 8
0 0 1
0 1 2
0 0.5 1
0.5 0 1
1 0 2
0.499999999488 0.499999999488 0
0.5 1 2
1 0.5 2
1 1 2
7 8 9 0
1 4 3 0
4 5 8 0
6 8 7 0
4 6 3 0
4 8 6 0
2 3 7 0
7 3 6 0
9 7 2
7 2 2
5 8 2
8 9 2
1 4 1
4 5 1
2 3 1
3 1 1

図 6: $m=2$ の時の三角形分割の様子 (Th.msh に対応)

マニュアルで確認していないが、 多分次のようなフォーマットになっているのであろう。

FreeFem++ のメッシュファイルのフォーマット

総節点数$n$    総要素数$m$     境界に属する辺の数 $N$
節点 $P_1$の$x$,$y$座標とラベル(0は内点)
    $\vdots$
節点 $P_{n}$の$x$,$y$座標とラベル(0は内点)
要素 $e_1$の3節点の節点番号と 0
要素 $e_2$の3節点の節点番号と 0
    $\vdots$
要素 $e_m$の3節点の節点番号と 0
境界に属する辺 $Q_1$とラベル
    $\vdots$
境界に属する辺 $Q_N$ とラベル

なお、square()³ という関数を使うと、 分割まで込めて菊地 [1] の例と同じように出来る。

poissno-kikuchi-square.edp

// poisson-kikuchi-square.edp
// https://m-katsurada.sakura.ne.jp/program/fem/poisson-kikuchi-square.edp
// 菊地文雄, 有限要素法概説, サイエンス社

int m=10;
mesh Th=square(m,m);
// plot(Th,wait=true,ps="Th.eps");
savemesh(Th,"Th.msh");
fespace Vh(Th,P1);
Vh u,v;
func f=1;
func g1=0;
func g2=0;
solve Poisson(u,v)=
  int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
 -int2d(Th)(f*v)
 -int1d(Th,2,3)(g2*v)
 +on(1,4,u=g1);
plot(u,wait=1,ps="poisson-kikuchi-square.eps");

//3次元鳥瞰図
//real [int] levels =0.0:0.01:1.0;
//plot(u,dim=3,viso=levels,fill=true,wait=true);

図 7: $m=10$ の時の三角形分割の様子