2.2 簡単な問題で数学超特急

Poisson 方程式の境界値問題で説明します (有限要素法を自習したい場合には、 菊地文雄, 『有限要素法概説』, サイエンス社, という参考書がイチオシです)。

$\R^2$ 内の領域 (連結開集合) $\Omega$ における Poisson 方程式の Dirichlet 問題

$$-\Laplacian u=f \mbox{(in $\Omega$)} ,$$ (PE)

$$u=0 \mbox{(on $\Gamma:=\rd\Omega$)}$$ (DBC)

を考える (弱解の方法の例題として、もっとも簡単な、定番の問題です)。

Poisson 方程式に $v\in C^\infty_0(\Omega)$ ( $C^\infty_0(\Omega)$ は、 $\Omega$ 内に compact な台を持つ $C^\infty$ 級の関数全体) をかけて、Green の積分公式 (多次元版部分積分) を用いると、 次式が得られます。

$$\dint_\Omega \left(\frac{\rd u}{\rd x}\frac{\rd v}{\rd x} +\frac{\rd u}{\rd y}\frac{\rd v}{\rd y} \right) \DxDy =\dint_\Omega f(x,y)v(x,y)\;\DxDy \mbox{($v\in C^\infty_0(\Omega)$)} .$$ (1)

逆に $u=0$ (on $\Gamma$ ) を満たす滑らかな $u$ が、 この条件を満たせば、$u$ は Poisson 方程式を満たすことも容易に分かります。

微分方程式を満たす $u$ を求める代りに、 (1) を満たす $u$ を見出すことを考えましょう。 解の存在を容易に保証できるようにするため、 関数空間を完備化するのが便利です (解を極限の論法で得よう、という解析学の常套手段)。 具体的には、 以下に定義する $H^1_0(\Omega)$ というソボレフ空間 (一般化された導関数を持つ関数からなる関数空間の一種) で $u$ を探すことにします。

(PE),(DBC) の弱解の定義

$u\in H^1_0(\Omega)$ かつ

$$\dint_{\Omega} \left( \frac{\rd u}{\rd x}\frac{\rd v}{\rd x} +\fr... ... u}{\rd y}\frac{\rd v}{\rd y} \right) \DxDy =\dint_{\Omega} f(x,y)v(x,y)\;\DxDy \mbox{($v\in H^1_0(\Omega)$)} .$$

$H^1_0(\Omega)$ とは

$$H^1(\Omega) =\left\{u\in L^2(\Omega); \frac{\rd u}{\rd x_j}\in L^2(\Omega) (j=1,2)\right\}$$

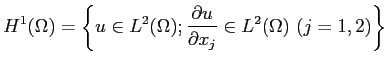
という関数の集合に

$$(u,v)_{H^1}:=\dint_\Omega u(x,y)\overline{v(x,y)}\;\DxDy +\dint_{\Omega} \nabla u(x,y)\cdot\overline{\nabla v(x,y)}\;\DxDy$$

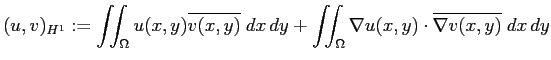
という内積を導入すると、 $H^1(\Omega)$ は Hilbert 空間 (完備な内積空間) になる。

$$H^1_0(\Omega):=$$$$\mbox{$C^\infty_0(\Omega)$ の $H^1(\Omega)$ での閉包}$$

とおく。 $H^1_0(\Omega)$ の要素は、 $H^1(\Omega)$ の要素のうちで、 ある意味で $\Gamma$ 上 0 となるものとみなすことができる。

$\Omega$ を三角形の「整った」合併 $T_h$ で近似し、 $T_h$ で連続で、 各三角形上で1次関数であるような関数全体を $V_h$ とします。 $V_h$ は $H^1(\Omega)$ の有限次元部分空間とみなせ、 グラフが三角錐であるような関数 $\varphi_1$ , $\dots$ , $\varphi_m$ を 基底に取って、 各元をその基底の線型結合として表現することができます:

$$V_h=\left\{\sum_{j=1}^m c_j\varphi_j;(c_j)\in\R^m\right\}.$$

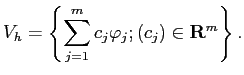
(PE),(DBC) の弱解の定義 (書き換え)

$u\in H^1(\Omega)$ かつ

$$\dint_{\Omega} \left( \frac{\rd u}{\rd x}\frac{\rd v}{\rd x} +\fr... ... u}{\rd y}\frac{\rd v}{\rd y} \right) \DxDy =\dint_{\Omega} f(x,y)v(x,y)\;\DxDy \mbox{($v\in H^1(\Omega)$, $v=0$ on $\Gamma$)} ,$$

$$u=0 \mbox{(on $\Gamma$)} .$$

有限要素解の定義

$u_h\in V_h$ かつ

$$\dint_{T_h} \left( \frac{\rd u_h}{\rd x}\frac{\rd v_h}{\rd x} +\f... ...h}{\rd y}\frac{\rd v_h}{\rd y} \right) \DxDy =\dint_{T_h} f(x,y)v_h(x,y)\;\DxDy \mbox{($v_h\in V_h$, $v_h=0$ on $\Gamma$)} ,$$

$$u_h=0 \mbox{(on $\Gamma$)} .$$

次のようなプログラム poisson.edp を用意します (例えば emacs を使って作成します)。

poisson.edp

// 境界の定義 (単位円), いわゆる正の向き
border Gamma(t=0,2*pi) { x=cos(t); y=sin(t); }
// 三角形要素分割を生成 (境界を50に分割) 
mesh Th = buildmesh(Gamma(50));
plot(Th,wait=true);
// 有限要素空間は P1 (区分的１次多項式) 要素
real [int] levels =-0.012:0.001:0.012;
fespace Vh(Th,P1);
Vh u,v;
// Poisson 方程式 -△u=f の右辺
func f = x*y;
// 現在時刻をメモ
real start = clock();
// 問題を解く
solve Poisson(u,v)
 = int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))-int2d(Th)(f*v)
   +on(Gamma,u=0);
// 可視化 (等高線)
plot(u,wait=true);
//plot(u,viso=levels,fill=true,wait=true);
// 可視化 (3次元) --- マウスで使って動かせる
plot(u,dim=3,wait=true);
//plot(u,dim=3,viso=levels,fill=true,wait=true);
// 計算時間を表示
cout << " CPU time= " << clock() - start << endl;

FreeFem++ で poisson.edp を実行

mymac% FreeFem++ poisson.edp

キーボードからのコマンド

[Enter]	次のプロットへ
[ESC]	グラフィックスを閉じる
$+$	ズーム（イン）する
$-$	ズームアウトする
=	ズームの状態を元に戻す
c	ベクトルの矢印の大きさを短くする
C	ベクトルの矢印の大きさを長くする
r	リフレッシュする
f	カラーを塗りつぶすかどうか
v
?	help

plot(u); のところを plot(u,ps="graph.eps"); のように すると、画面に表示するだけでなく、 PostScript 形式でファイル出力できます (TEX 文書への取り込みが簡単です)。

図: 円盤領域で Poisson 方程式 $-\Laplacian u(x,y)=x y$ の同次 Dirichlet 問題を解く (要素分割と解の等高線)

図 2: dim=3 でグラフの鳥瞰図を描く