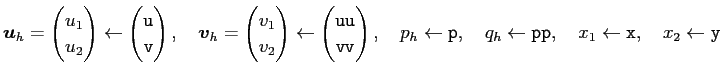
// stokes.edp (in the manual, chapter 3) int n=3; mesh Th=square(10*n,10*n); plot(Th, wait=1, ps="stokes-p1b-mesh.eps"); fespace Uh(Th,P1b); Uh u,v,uu,vv; fespace Ph(Th,P1); Ph p,pp; solve stokes([u,v,p],[uu,vv,pp]) = int2d(Th)(dx(u)*dx(uu)+dy(u)*dy(uu) + dx(v)*dx(vv)+ dy(v)*dy(vv) + dx(p)*uu + dy(p)*vv + pp*(dx(u)+dy(v))) + on(1,2,4,u=0,v=0) + on(3,u=1,v=0); plot([u,v],p,wait=1,ps="stokes-p1b-solution.eps"); |
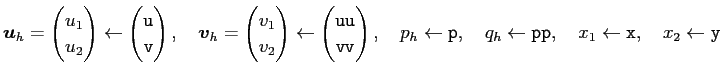
とすると、
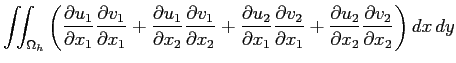 | ||
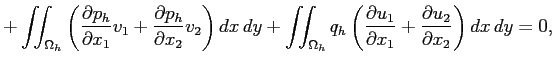 |
これは
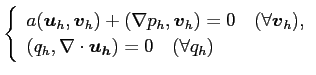
と同値である。
第2項が
![]() でないところが目につく。
そうするためには
でないところが目につく。
そうするためには
int2d(Th)(dx(u)*dx(uu)+dy(u)*dy(uu) + dx(v)*dx(vv)+ dy(v)*dy(vv) -p*(dx(uu)+dy(vv))+ dy(p)*vv + pp*(dx(u)+dy(v))) + on(1,2,4,u=0,v=0) + on(3,u=1,v=0); |
とにかく P1b/P1 を採用した結果は、 図 6 となる。
P1/P1 にすると上手く計算できないことは常識とされているが、 自分でプログラムを書く場合、なかなかそこまで試す気にはなれない。 しかし FreeFem++ でそれをするのは簡単である (図 7)。
P2/P1 は、良く知られているようにきちんと解ける (図 8)。
他にも、悪い冗談のようだが P2/P2 などが気軽に試せる。
当り前かもしれないが、弱形式を少しいじっただけで結果がコロコロ変わる。