Next: 6 Laplace-Beltrami Сйюућеу┤асЂе ТгАтЁЃ Up: Laplacian сЂеТЦхт║ДТеЎ Previous: сѓ░сЃфсЃ╝сЃ│сЂ«тЁгт╝ЈсѓњтѕЕућесЂЎсѓІТќ╣Т│Ћ
сЂЎсЂДсЂФСйЋт║дсѓѓУдІсЂЪсѓѕсЂєсЂФсђЂ![]() сЂФсЂісЂЉсѓІ Laplacian сЂ«ТЦхт║ДТеЎУАеуц║
сЂФсЂісЂЉсѓІ Laplacian сЂ«ТЦхт║ДТеЎУАеуц║
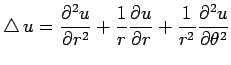
![]()
![]() ,
, ![]() (
(![]() ) сЂеуЏ┤УДњт║ДТеЎу│╗сЂФсЂЮсЂБсЂдТа╝тГљсѓњтЁЦсѓїсЂЪ
та┤тљѕсђЂ
) сЂеуЏ┤УДњт║ДТеЎу│╗сЂФсЂЮсЂБсЂдТа╝тГљсѓњтЁЦсѓїсЂЪ
та┤тљѕсђЂ
ТЦхт║ДТеЎ
![]() сЂ«уЕ║жќЊсѓњсђЂУДњт║дТќ╣тљЉсЂФ
сЂ«уЕ║жќЊсѓњсђЂУДњт║дТќ╣тљЉсЂФ
![]() уГЅтѕєсЂЌсЂдсђЂ
уГЅтѕєсЂЌсЂдсђЂ
![$\displaystyle \Laplacian u(0,0)
\kinji
\frac{4}{h_r^2}
\left[
\frac{u_{1,0}+u_{1,N}+u_{1,2N}+u_{1,3N}}{4}-u(0,0)
\right]
$](img187.png)
![$\displaystyle \Laplacian u(0,0)
\kinji
\frac{4}{h_r^2}
\left[
\frac{u_{1,j}+u_{1,j+N}+u_{1,j+2N}+u_{1,j+3N}}{4}-u(0,0)
\right]
$](img189.png)
сЂЊсѓїсЂІсѓЅ
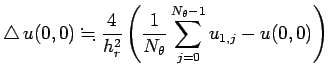 |
(5) |
сЂЊсѓїсЂ»СИђУѕгТгАтЁЃсЂФТІАт╝хсЂДсЂЇсѓІ: ![]() сЂФсЂісЂЉсѓІ Laplacian сЂ«У┐ЉС╝╝сЂесЂЌсЂд
сЂФсЂісЂЉсѓІ Laplacian сЂ«У┐ЉС╝╝сЂесЂЌсЂд
![$\displaystyle \Laplacian u(0)\kinji \frac{2\times(\mbox{уЕ║жќЊсЂ«ТгАтЁЃ})}{h_r^...
...ФсЂісЂЉсѓІ $u$\ сЂ«т╣│тЮЄтђц}) -(\mbox{тјЪуѓ╣сЂФсЂісЂЉсѓІ $u$\ сЂ«тђц})\right].$](img191.png) |
(6) |