4.7.3 実験例: 爆発する問題を RKF45 で計算

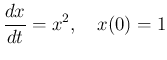
(かなりいい加減なプログラムであるが、 あえてここに含める理由の一つは、 公式中の係数に書き間違いがないことを確認できるようにするためである。)

/*
 * rkf.c --- RKF45 のサンプル (まだ未完成です)
 */

#include <math.h>

#define RKF45_STAGE 6

static double rkf45_alpha[RKF45_STAGE] = {
  0.0, 1.0/4, 3.0/8, 12.0/13, 1.0, 1.0/2};

static double rkf45_beta[RKF45_STAGE][RKF45_STAGE-1] = {
  {   0.0,          0.0,                      0.0,        0.0},
  {   1.0/4,        0.0,                      0.0,        0.0},
  {   3.0/32,       9.0/32,                   0.0,        0.0},
  {1932.0/2197, -7200.0/2197, 7296.0/2197,    0.0,        0.0},
  { 439.0/216,     -8.0,      3680.0/513,  -845.0/4104,   0.0},
  {  -8.0/27,       2.0,     -3544.0/2565, 1859.0/4104, -11.0/40}
};

static double rkf45_mu[RKF45_STAGE] = {
  16.0/135, 0.0, 6656.0/12825, 28561.0/56430, -9.0/50, 2.0/55
};

static double rkf45_mu2[RKF45_STAGE] = {
  25.0/216, 0.0, 1408.0/2565, 2197.0/4104, -1.0/5
};

double sum(int n, double *x)
{
  int i;
  double s = 0;
  for (i = 0; i < n; i++) s += x[i];
  return s;
}

/* 簡単なチェック */
void check_table()
{
  int i;
  for (i = 0; i < RKF45_STAGE; i++)
    printf("%g %g\n", rkf45_alpha[i], sum(i, rkf45_beta[i]));
  printf("rkf45_muの和=%g\n", sum(RKF45_STAGE, rkf45_mu));
  printf("rkf45_mu2の和=%g\n", sum(RKF45_STAGE, rkf45_mu2));
}

double dotprod(int n, double *x, double *y)
{
  int i;
  double s = 0;
  for (i = 0; i < n; i++) s += x[i] * y[i];
  return s;
}

/*
 * RKF45 で時刻 *t から、1ステップ進む
 * 特に問題なければ *hh だけ進むが、単位長さあたりの許容誤差限界 eps_tol
 * (解説のε/Hに相当) を達成するために、必要ならば刻み幅の自動調節をする。
 */
int rkf45(double *newx,
	  double *t, double x, double *hh, double hmin, double eps_tol,
	  double f(double, double))
{
  int i, s = RKF45_STAGE;
  double k[RKF45_STAGE], newx1, newx2, h = *hh, error;
  do {
    /* k1,k2,k3,k4,k5,k6 を計算する */
    for (i = 0; i < s; i++)
      k[i] = h * f(*t + rkf45_alpha[i] * h, x + dotprod(i, rkf45_beta[i], k));
    /* 5次精度, 4次精度の値を計算 */
    newx1 = x + dotprod(s, rkf45_mu, k);
    newx2 = x + dotprod(s, rkf45_mu2, k);
    /* 見積誤差 */
    error = fabs(newx1 - newx2);
    if (error < eps_tol) {
      *newx = newx2;
      *hh = h;
      *t += h;
      return 0;
    }
    // 新h = 0.8 h (ε h/ (H 誤差見積)^(1/4)
    h = 0.8 * h * pow(eps_tol * h / error, 0.25);
  }
  while (h > hmin);
  printf("h=%g<=hmin=%g\n", h, hmin);
  return 1;
}

double f(double t, double x)
{
  return x * x;
}

int main()
{
  int n = 1000;
  double a, b, x, h, hmin, t;
  check_table();
  a = 0; b = 1; h = (b - a) / n; hmin = h / 100000;
  x = 1;
  t = 0;
  while (t < 1.0) {
    if (t + h > 1.0) h = 1.0 - t;
    if (rkf45(&x, &t, x, &h, hmin, 1e-13, f) != 0) {
      fprintf(stderr, "誤差が小さくならない\n");
      exit(1);
    }
    printf("t=%25.16f, x=%25.16g\n", t, x);
  }
  printf("%25.16g\n", x);
  return 0;
}

このプログラムでは爆発の例に出した初期値問題

$$\frac{\Dx}{\Dt}=x^2,\quad x(0)=1$$

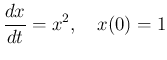
を解いているが、 (実行してみると¹²) 爆発時刻 $t=1$ のところで、刻み幅がどんどん小さくなっていくのが分かる。

なお、具体的な時間刻み幅の制御について具体的に書いてある本は多くない (そのためもあって、 私自身よく分かっていない部分もあり、上記のプログラムも完成品ではない)。 その点で森 [8] は貴重である。 そこに掲載されているプログラムのアルゴリズムは (FORTRAN プログラムを C 風に書き直して示せば) 以下のようなものである (と思う。読み違いが無ければ。)。 なるほどと思うところもあるが、今一つ納得できていないところもある。

  maxiter = 100;
  epsmac = 1e-15;
  // t0 から tn まで解く
  // eps は許容絶対誤差、epsmac は計算機イプシロン程度の数
  epsv = max(eps, epsmac); // はて、相対誤差ならともかく、絶対誤差で筋が通る?
  // eb は単位時間当り許される誤差
  eb = fabs(epsv / (tn - t0));
  //
  t = t0;
  h = tn - t0;
  //
  for (iter = 1; iter <= itermax; iter++) {
    // とにかく刻み幅 h で進んでみて、局所打ち切り誤差の推定もする
    rkf(t, h, x0, &xn, &errmax);
    // 推定誤差が時間刻み幅 h あたりの許容誤差よりも小さいかどうかチェック
    if (errmax <= fabs(eb*h)) { // 小さい場合
      // 時刻を進める
      t += h;
      // 進んだ分だけ残り時間は減らす (最終時刻 - 現在時刻)
      h = tn - t;
      // 残り時間がなければ (計算しきったら) 戻る
      if (fabs(h) <= epsmac)
        return;
      // まだ残り時間があれば続行
      x0 = xn;
    }
    else {
      // 推定誤差が時間刻み幅 h あたりの許容誤差よりも大きい場合
      // 推定誤差と許容絶対誤差の大小を比較
      if (errmax > epsv)
        // 推定誤差が許容絶対誤差より大きければ刻み幅を一気に 10% に縮める
        h *= 0.1;
      else {
        h *= 0.9 * sqrt(sqrt(eb * fabs(h) / errmax));
        if (fabs(h) < epsmax)
          break;
        }
      }
    }
  }
  fprintf(stderr,
         "rkf45(): t=%g で困難に出会いました。計算を中断します。", t);
  return 1;

(なお、この手の問題のシミュレーションについては、 伊理・藤野 [9] にも何か書いてあったような気がする。 陳蘊剛さんの爆発のシミュレーションはどうだったかな… そのうちに一度まじめに調べてみよう。まあ、これは独り言みたいなものです。)