![]() から
から ![]() まで、誤差の大きさの見積が、
計算者が指定した値
まで、誤差の大きさの見積が、
計算者が指定した値 ![]() より小さくなるように解くことを目標にする。
このとき
より小さくなるように解くことを目標にする。
このとき ![]() のことを許容誤差限界と呼ぶ。
のことを許容誤差限界と呼ぶ。
![]() を
を
![]() と分割して解くことにする。
と分割して解くことにする。
![]() における値
における値 ![]() まで定まったとする。
まで定まったとする。
![]() における 5次公式, 4 次公式による近似値をそれぞれ
における 5次公式, 4 次公式による近似値をそれぞれ
![]() ,
, ![]() とすると、
とすると、
となる。ただし
通常は、
さて、
と置いておく。
目標は ![]() で解いたときの許容誤差限界を
で解いたときの許容誤差限界を ![]() とすることであるから、
とすることであるから、
![]() で解いたときの許容誤差限界は
で解いたときの許容誤差限界は
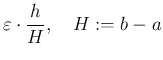
とするのが妥当であろう。それゆえ
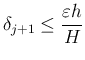
であれば良いが、 そうでない場合は、
とおき、これに対応した
となると期待できるから、
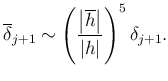
今度は
![]() となって欲しいわけだが、
この不等式の左辺に推定値を代入した不等式
となって欲しいわけだが、
この不等式の左辺に推定値を代入した不等式
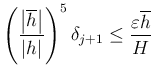
を
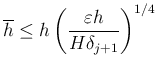
を得る。安全のために
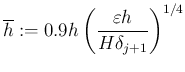
で