Next: 5.1.2.2 ちょっと詳しく解説 Up: 5.1.2 平衡点と線形化 Previous: 5.1.2 平衡点と線形化
| (2) | 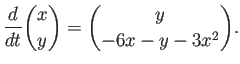 |
まず最初に平衡点を求めましょう。方程式の右辺のベクトル値関数 ![]() が
0 になるという条件、つまり連立方程式
が
0 になるという条件、つまり連立方程式
さて、これを実行するには前回のプログラムをちょっと修正すれば OK です。 そうして作ったプログラムreidai8a.fを用意してあります。いつもの ようにgetsampleコマンドで手元にコピーした後に、コンパイルして実 行してみましょう。ここではサンプルの入力データを収めたファイルrei8a.data もありますので、それを使って試すことにすれば、
| ターミナルで実行 (入手, コンパイル, 実行) |
curl -O http://nalab.mind.meiji.ac.jp/~mk/program/ode_prog/reidai8a-glsc.c cglsc reidai8a-glsc.c ./reidai8a-glsc.c 範囲(xleft,ybottom,xright,ytop)? -4 -4 4 4 |
curl -O http://nalab.mind.meiji.ac.jp/~mk/program/ode_prog/rei8a.data cat rei8a.data | ./reidai8a-glsc |
![]() の回りでは安定渦状点、
の回りでは安定渦状点、
![]() の回りでは不安定結
節点のような流れになっています。
の回りでは不安定結
節点のような流れになっています。
大事なことは二つあって、一つは
% ./reidai8a-glsc 範囲(xleft,ybottom,xright,ytop)? -100 -100 100 100 したいことを番号で選んで下さい。 -1:メニュー終了, 0:初期値のキーボード入力, 1:初期値のマウス入力, 2:change h,T(h= 0.0100,T=10.0000) 1 マウスの左ボタンで初期値を指定して下さい(右ボタンで中止)。
もう一つの大事なことは、平衡点の周囲の流れがどうなるかは、
微分法を使ってある程度まで解析できるということです。
上の例題の右辺の ![]() を微分してヤコビ行列を作ると、
を微分してヤコビ行列を作ると、
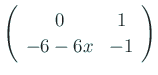
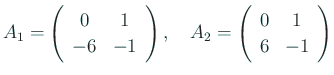
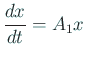 の原点での流れに、
の原点での流れに、
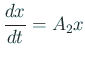 の原点での流れに似ている、ということです。
の原点での流れに似ている、ということです。