Next: A.5.3.0.1 з¬ҰеҸ·гҒ®еӨүеҢ–ж•°гҒ®иЁҲз®—гҒ«й–ўгҒҷгӮӢжіЁж„Ҹ Up: A.5 Strum гҒ®ж–№жі• Previous: A.5.2 гғҰгғјгӮҜгғӘгғғгғүгҒ®дә’йҷӨжі•гҒ«гӮҲгӮӢ Strum еҲ—гҒ®з”ҹжҲҗ
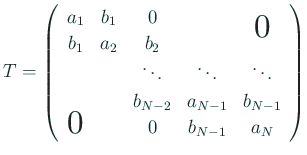
![\begin{jremark}[гҒЎгӮҮгҒЈгҒЁгҒ—гҒҹ]
е®ҹгҒҜд»ҘдёӢгҒ®иӯ°и«–гҒ§ $T$ гҒ®еҜҫз§°жҖ§г...
...гҒ§гҖҒгҒҫгҒӮеҝ…гҒҡгҒӨгҒ„
гҒҰгҒҸгӮӢгҖҢгҒҠгҒҫгҒ‘гҖҚгҒ§гҒҷгҒӘгҖӮ \qed
\end{jremark}](img460.gif)
![]() (
(
![]() ) гҒЁд»®е®ҡгҒҷгӮӢгҖӮгӮӮгҒ—гҒӮгӮӢ
) гҒЁд»®е®ҡгҒҷгӮӢгҖӮгӮӮгҒ—гҒӮгӮӢ ![]() гҒ«еҜҫгҒ—гҒҰ
гҒ«еҜҫгҒ—гҒҰ
![]() гҒӘгӮүгҒ°
гҒӘгӮүгҒ°
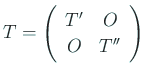
![]() гӮ’
гӮ’
![]() гҒ®з¬¬
гҒ®з¬¬ ![]() дё»еә§иЎҢеҲ—ејҸгҒЁгҒҷгӮӢ
(
дё»еә§иЎҢеҲ—ејҸгҒЁгҒҷгӮӢ
(
![]() )гҖӮгҒҷгҒӘгӮҸгҒЎ
)гҖӮгҒҷгҒӘгӮҸгҒЎ
гҒҹгҒ гҒ—гҖҒ
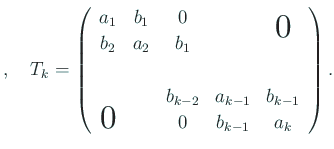
![\begin{jlemma}
% latex2html id marker 1220 [жјёеҢ–ејҸ]
(\ref{eq:pkгҒ®е®ҡзҫ©}) г...
...mbda) & = & \det(\lambda I-T).
\end{array}\right.
\end{displaymath}\end{jlemma}](img473.gif)
|
![\begin{jlemma}
% latex2html id marker 1236 [Strum еҲ—гҒ§гҒӮгӮӢгҒ“гҒЁ]
(\ref{eq:...
...$ гҒӘгӮүгҒ° $p_N'(\lambda_0)
p_{N-1}(\lambda_0)>0$.
\end{enumerate}\end{jlemma}](img474.gif)
|