Next: 3.1.1 非同次Neumann境界値問題 Up: 3 2次元Poisson方程式 Previous: 3 2次元Poisson方程式
まずは同次Dirichlet境界値問題のプログラムを示す。
長方形領域
![]() における Poisson 方程式の境界値問題
における Poisson 方程式の境界値問題
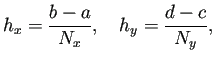 |
||
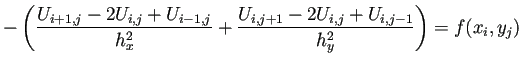 |
(1) | |
| (
|
||
| (2) | ||
| (3) |
Dirichlet 境界値問題については、
![]() (
(
![]() ,
,
![]() ) が未知数になる。
桂田 [2] というノートでは
) が未知数になる。
桂田 [2] というノートでは
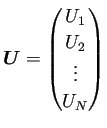 を未知ベクトルとする連立1次方程式を考えた。
連立1次方程式の係数行列は
を未知ベクトルとする連立1次方程式を考えた。
連立1次方程式の係数行列は
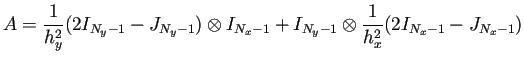
以下のプログラムでは (4) の代わりに
| (5) |
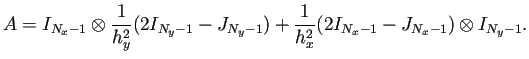
| poisson_coef.m |
function A=poisson_coef(W, H, nx, ny) % 長方形領域 (0,W)×(0,H) における Poisson 方程式の Dirichlet 境界値問題 % Laplacian を差分近似した行列を求める。 % 長方形を nx×ny 個の格子に分割して差分近似する。 % MATLABでは % (1) 行列は Fotran と同様の column first であり、 % (2) mesh(), contour() による「行列描画」は Z(j,i) と添字の順が普通と逆なので、 % l=i+(j-1)*(nx-1) と row first となるように1次元的番号付けする hx=W/nx; hy=H/ny; m=nx-1; n=ny-1; ex=ones(nx,1); ey=ones(ny,1); Lx=spdiags([-ex,2*ex,-ex],-1:1,m,m)/(hx*hx); Ly=spdiags([-ey,2*ey,-ey],-1:1,n,n)/(hy*hy); A=kron(speye(m,m),Ly)+kron(Lx,speye(n,n)); |
| poisson2d.m |
% 長方形領域 (0,W)×(0,H) で Poisson 方程式の同次Dirichlet境界値問題を解く
W=3.0;
H=2.0;
nx=30;
ny=20;
m=nx-1;
n=ny-1;
% 連立方程式を作成して解く
% MATLABの行列は Fotran と同様の column first であり、
%「行列描画」は Z(j,i) と添字の順が普通と逆なので、
% l=i+(j-1)*(nx-1) と row first となるように1次元的番号付けする
A=poisson_coef(W, H, nx, ny);
%
x=linspace(0,W,nx+1); % x=[x_0,x_1,...,x_nx]
y=linspace(0,H,ny+1); % y=[y_0,y_1,...,y_ny]
[X,Y]=meshgrid(x,y);
% f≡1 の場合
%F=ones(m*n,1);
f=-2*(X.^2-3*X+Y.^2-2*Y);
f=f(2:ny,2:nx);
F=f(:);
%
U=zeros(n,m);
U(:)=A\F;
% 境界値0をつける
u=zeros(ny+1,nx+1);
u(2:ny,2:nx)=U;
%
% グラフの鳥瞰図
clf
colormap hsv
subplot(1,2,1);
mesh(X,Y,u);
colorbar
% 等高線
subplot(1,2,2);
contour(X,Y,u);
%
disp('図を保存する');
print -dpdf poisson2d.pdf % 利用できるフォーマットは doc print で分かる
print -dpng poisson2d.png % 利用できるフォーマットは doc print で分かる
print -deps poisson2d.eps % 利用できるフォーマットは doc print で分かる
|
まったく別の時期に作ったプログラム。 ほとんど同じで我ながら唖然とする。 最初のプログラムが mesh() と contour() で、 鳥瞰図と等高線を別々に描いたが、 こちらは meshc() で同時に描いている。
| poisson2d_v2.m |
% poisson2d.m --- Poisson equation -△u=sin(π x)sin(2π y) (0<x<3, 0<y<2), u=0
% [0,3]×[0,2]を 30×20 に分割する
a=0; b=3; c=0; d=2;
nx=30; ny=20;
%nx=6; ny=4;
X=linspace(a,b,nx+1);
Y=linspace(c,d,ny+1);
[x,y]=meshgrid(X,Y);
% f(x,y)=sin(x)sin(2y)
F=sin(pi*x).*sin(2*pi*y);
% 係数行列
hx=(b-a)/nx; hy=(d-c)/ny;
e=ones(nx-1,1);
ax=spdiags([-e 2*e -e],-1:1,nx-1,nx-1)/(hx*hx);
e=ones(ny-1,1);
ay=spdiags([-e 2*e -e],-1:1,ny-1,ny-1)/(hy*hy);
a=kron(speye(nx-1),ay)+kron(ax,speye(ny-1));
% F の境界部分の値を削除して、1次元化
f=F(2:end-1,2:end-1);
f=f(:);
%
u=zeros(ny+1,nx+1);
u(2:end-1,2:end-1)=reshape(a\f,ny-1,nx-1);
%
figure('Name','Poisson equation -△u=sin(π x)sin(2π y) (0<x<3, 0<y<2)')
meshc(x,y,u)
figure(gcf)
|