Next: B..2.2 2次元の場合 Up: B..2 Laplacianの近似 Previous: B..2 Laplacianの近似
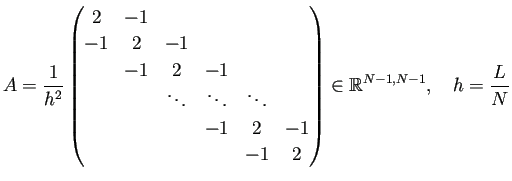
h=L/N; e=ones(N-1,1); a=spdiags([-e 2*e -e],-1:1,N-1,N-1)/(h*h); |
ずっと以前は、疎行列関係の命令を知らずに次のように作っていた。
h=L/N; e=ones(N-1,1); a=(2*eye(N-1,N-1)-diag(e,1)-diag(e,-1))/(h*h);(この後で、遅ればせながら a=sparse(a); としてメモリを節約するという手はあるかも。) |