next up previous contents
Next: C. 応用: 熱方程式の初期値境界値問題 Up: B. 素朴に常微分方程式の初期値問題 Previous: B..2 分けて書いてみる

B..3 投げたボールのバウンド

(C++ http://nalab.mind.meiji.ac.jp/~mk/labo/text/welcome-to-eigen/node2.htmlの焼き直し版である。という訳で説明は省略させてもらう。 図を観ると何となく分かる？)

ballbound.jl

# ballbound.jl --- 投げたボールのバウンド, 空気抵抗ありのシミュレーション

# Runge-Kutta 法の1ステップ
function rungekutta(f,t,x,dt)
  k1=dt*f(t,x)
  k2=dt*f(t+dt/2, x+k1/2)
  k3=dt*f(t+dt/2, x+k2/2)
  k4=dt*f(t+dt, x+k3)
  x + (k1 + 2 * k2 + 2 * k3 + k4) / 6
end

function f(t,x)
  Gamma=1.0
  m=100.0
  g=9.8
  y=similar(x)
  y[1] = x[3]
  y[2] = x[4]
  y[3] = -Gamma/m*x[3]
  y[4] = -g-Gamma/m*x[4]
  y
end

function ballbound(n=1000) # 1000等分くらい
  t=0.0
  v0=50.0
  theta=50.0
  x=[0.0,0.0,v0*cos(theta*pi/180),v0*sin(theta*pi/180)]
  println("t x")
  println("$t $x")
  Tmax=20.0
  dt=Tmax/n
  println("Tmax=$Tmax, dt=$dt")
  s=@sprintf "%f %f %f %f %f\n" t x[1] x[2] x[3] x[4]
  print(s)
  of = open("ballbound.dat","w")
  print(of,s)
  for i=1:n
    # x=euler(f,t,x,dt)
    x=rungekutta(f,t,x,dt)
    if x[2]<0
      x[2] = - x[2]
      x[4] = - x[4]
    end
    t=i*dt
    s=@sprintf "%f %f %f %f %f\n" t x[1] x[2] x[3] x[4]
    print(s)
    print(of,s)
  end
  close(of)
  # 以下は工事中
  of = open("ballbound.gp","w")
  println(of,"plot \"ballbound.dat\" using 2:3 with lp")
  close(of)
  run(`gnuplot ballbound.gp`)
end

図 2: バウンドの処理はイイカゲンだけど
Image ballbound

上のプログラムは一度データをファイルに書き出してから描画している。 直接 gnuplot と通信して描画するプログラムも紹介しておく。
http://nalab.mind.meiji.ac.jp/~mk/misc/20191228/ballbound-v3.jl

# ballbound-v3.jl --- 投げたボールのバウンド, 空気抵抗ありのシミュレーション

# Runge-Kutta 法の1ステップ
function rungekutta(f,t,x,dt)
  k1=dt*f(t,x)
  k2=dt*f(t+dt/2, x+k1/2)
  k3=dt*f(t+dt/2, x+k2/2)
  k4=dt*f(t+dt, x+k3)
  x + (k1 + 2 * k2 + 2 * k3 + k4) / 6
end

function f(t,x)
  Gamma=1.0
  m=100.0
  g=9.8
  y=similar(x)
  y[1] = x[3]
  y[2] = x[4]
  y[3] = -Gamma/m*x[3]
  y[4] = -g-Gamma/m*x[4]
  y
end

function ballbound3(n=1000) # 1000等分くらい
  t=0.0
  v0=50.0
  theta=50.0
  x=[0.0,0.0,v0*cos(theta*pi/180),v0*sin(theta*pi/180)]
  println("t x")
  println("$t $x")
  Tmax=20.0
  dt=Tmax/n

  println("Tmax=$Tmax, dt=$dt")
  p=open(pipeline(`gnuplot --persist`; stderr=Pipe()), "r+")
  println(p.in, "plot '-' with lines title \"n=$n\"");

  println(p.in, "$(x[1]) $(x[2])")
  for i=1:n
    # x=euler(f,t,x,dt)
    x=rungekutta(f,t,x,dt)
    if x[2]<0
      x[2] = - x[2]
      x[4] = - x[4]
    end
    t=i*dt
    # @printf(p.in, "%f %f\n", x[1], x[2])
    println(p.in, "$(x[1]) $(x[2])")
  end
  println(p.in, "e")
  flush(p.in)
  println(p.in, "set term png");
  println(p.in, "set output \"ballbound3.png\"");
  println(p.in, "replot");
  println(p.in, "quit")
  flush(p.in)
  close(p)
end

Julia, gnuplot, curl があれば…
$ curl -O http://nalab.mind.meiji.ac.jp/~mk/misc/20191228/ballbound-v3.jl
$ julia
julia> include("ballbound-v3.jl")
julia> ballbound3(1000)

常微分方程式の初期値問題の数値計算については、 利用できるものが色々ある。

数値計算は苦手のように思われている Mathematica で解いている人も少なくない。

一方で、数値計算の方法自体も学ぶに価するので、 そうしたときは、 「自分でプログラムを書いてみても良いんじゃないの」ということにしている。


ここから後は私の独自見解かもしれないが、そんなにズレていない自信がある。

常微分方程式の初期値問題の数値計算をする場合、 C言語でプログラムを書くことは勧めない。
その理由は、C は言語自体にベクトルを扱う機能がないから、である。
C 言語を使うくらいなら、代わりに C++ の利用を検討しよう。

常微分方程式の初期値問題の数値計算という目的に、 Julia はなかなか向いていると思う。 動的型付けの機能を使うことによって、 $ x'(t)=x(t)$, $ x(0)=1$ という問題も、 ボール投げの問題も、Euler法、 Runge-Kutta 法の計算部分のコードは全く同じものを使うことが出来る。

Runge-Kutta法の数学的表記

      $\displaystyle k_1:=\Delta t f(t_j,x_j),$
      $\displaystyle k_2:=\Delta t f(t_j+\Delta t/2,x_j+k_1/2),$
      $\displaystyle k_3:=\Delta t f(t_j+\Delta t/2,x_j+k_2/2),$
      $\displaystyle k_4:=\Delta t f(t_j+\Delta t,x_j+k_3),$
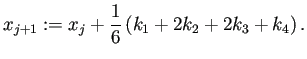      $\displaystyle x_{j+1}:=x_j+\frac{1}{6}\left(k_1+2k_2+2k_3+k_4\right).$

と Julia のコード 
# Runge-Kutta 法の1ステップ
function rungekutta(f,t,x,dt)
  k1=dt*f(t,x)
  k2=dt*f(t+dt/2, x+k1/2)
  k3=dt*f(t+dt/2, x+k2/2)
  k4=dt*f(t+dt, x+k3)
  x + (k1 + 2 * k2 + 2 * k3 + k4) / 6
end
の間の距離、何と短いことだろう。

それは大したことに感じられないかもしれないが、(古い規格の) Fortran, C を用いたプログラミング実習を手伝い・担当した経験を持っている身にとっては、 言語仕様の進歩の威力がひしひしと感じられる。


おまけ     Plots を使ったバージョンも載せておく。

ballbound_v4.jl

# ballbound_v4.jl --- 投げたボールのバウンド, 空気抵抗ありのシミュレーション
#=
curl -O http://nalab.mind.meiji.ac.jp/~mk/misc/20200102/ballbound_v4.jl
julia
ENV["GKS_ENCODING"] = "utf-8"
using Plots
gr()
include("ballbound_v4.jl")
ballbound_v4()
=#

# Runge-Kutta 法の1ステップ
function rungekutta(f,t,x,dt)
  k1=dt*f(t,x)
  k2=dt*f(t+dt/2, x+k1/2)
  k3=dt*f(t+dt/2, x+k2/2)
  k4=dt*f(t+dt, x+k3)
  x + (k1 + 2 * k2 + 2 * k3 + k4) / 6
end

function f(t,x)
  Gamma=1.0
  m=100.0
  g=9.8
  y=similar(x)
  y[1] = x[3]
  y[2] = x[4]
  y[3] = -Gamma/m*x[3]
  y[4] = -g-Gamma/m*x[4]
  y
end

function ballbound_v4(n=1000) # 1000等分くらい
  t=0.0
  v0=50.0
  theta=50.0
  x=[0.0,0.0,v0*cos(theta*pi/180),v0*sin(theta*pi/180)]
  println("t x")
  println("$t $x")
  Tmax=20.0
  dt=Tmax/n

  println("Tmax=$Tmax, dt=$dt")
  xs=zeros(n+1)
  ys=zeros(n+1)

  #println("$(x[1]) $(x[2])")
  xs[1] = x[1]; ys[1] = x[2]
  for i=1:n
    # x=euler(f,t,x,dt)
    x=rungekutta(f,t,x,dt)
    if x[2]<0
      x[2] = - x[2]
      x[4] = - x[4]
    end
    t=i*dt
    # @printf("%f %f\n", x[1], x[2])
    xs[i+1]=x[1]; ys[i+1] = x[2]
  end
  p=plot(xs,ys,title="速度に比例する抵抗を受けるボール投げ",
         xaxis=("x",(0.0,xs[n+1])),yaxis=("z",(0.0,findmax(ys)[1])))
  display(p)
  println("図を保存する")
  savefig("ballbound.pdf")
  savefig("ballbound.png")
  display(p)
end

グラフを描くこと自体はとても簡単だったが、 日本語タイトルをつけようとして、ちょっと苦戦した。 Plots と GR バックエンドでは日本語表示は出来ない、という書き込みも見た。 ENV["GKS_ENCODING"] = "utf-8" とすれば良い、 という情報を得て、無事表示出来たのだけれど…

試してみよう
$ curl -O http://nalab.mind.meiji.ac.jp/~mk/misc/20200102/ballbound_v4.jl
$ julia
julia> ENV["GKS_ENCODING"] = "utf-8"
julia> using Plots
julia> gr()
julia> include("ballbound_v4.jl")
julia> ballbound_v4()
日本語文字列をタイトルにする: https://github.com/JuliaPlots/Plots.jl/issues/791

図は、タイトルも含めて画面にはきちんと描くことができるが、 保存するときに GKS: invalid bitmap size と表示されて、 タイトルが化けたり、空白になったりする。 以下の図は、savefig() で保存したものではない。

図 3: 空気抵抗を受ける場合のボール投げ
Image ballbound_v4

もう一息なのかな？

next up previous contents
Next: C. 応用: 熱方程式の初期値境界値問題 Up: B. 素朴に常微分方程式の初期値問題 Previous: B..2 分けて書いてみる
桂田 祐史