Next: B..2 分けて書いてみる Up: B. 素朴に常微分方程式の初期値問題 Previous: B. 素朴に常微分方程式の初期値問題
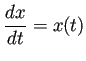 (
(
微分方程式の初期値問題
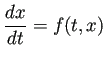 ( ( | ||
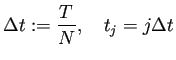 (
(
| testeuler.jl |
# testeuler.jl --- dx/dt=x (0<t<1), x(0)=1 を Euler法で解く
# using Printf が必要
function testeuler(Tmax=1.0,N=10)
# 初期値
t=0.0
x=1.0
@printf "t=%.4f x=%.7f exact=%.7f error=%.3e\n" t x exp(t) abs(exp(t)-x)
dt=Tmax/N
for j=1:N
x += dt * f(t,x)
t = j*dt
@printf "t=%.4f x=%.7f exact=%.7f error=%.3e\n" t x exp(t) abs(exp(t)-x)
end
end
function f(t,x)
x
end
|
| 実行例 |
julia> using Printf
julia> include("testeuler.jl")
julia> testeuler(1,10)
julia> testeuler(1,100)
|
実は
![]() ,
,
![]() となっている。
となっている。
![]() が
が
![]() に近いことが確かめられる。
に近いことが確かめられる。
Euler 法の次数は ![]() であり、
誤差
であり、
誤差
![]() であることも知られていて、
であることも知られていて、
![]() を変えることで確かめられる (
を変えることで確かめられる (![]() を
を ![]() 倍にすると誤差が
倍にすると誤差が
![]() 倍になる)。
倍になる)。
(4段4次)Runge-Kutta 法は
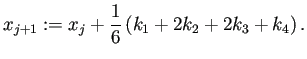 |
| testrungekutta.jl |
# testrungekutta.jl --- dx/dt=x (0<t<1), x(0)=1 を Runge-Kutta法で解く
# using Printf が必要
function testrungekutta(Tmax=1.0,N=10)
# 初期値
t=0.0
x=1.0
@printf "t=%.4f x=%.7f exact=%.7f error=%.3e\n" t x exp(t) abs(exp(t)-x)
# Runge-Kutta法
dt=Tmax/N
for j=1:N
k1=dt*f(t,x)
k2=dt*f(t+dt/2, x+k1/2)
k3=dt*f(t+dt/2, x+k2/2)
k4=dt*f(t+dt, x+k3)
x += (k1+2*k2+2*k3+k4) / 6
t = j * dt
@printf "t=%.4f x=%.7f exact=%.7f error=%.3e\n" t x exp(t) abs(exp(t)-x)
end
end
function f(t,x)
x
end
|
| 実行例 |
julia> using Printf
julia> include("testrungekutta.jl")
julia> testrungekutta(1,10)
julia> testrungekutta(1,100)
|
実は
![]() となっている。
誤差
となっている。
誤差
![]() であることが知られている。
であることが知られている。
![]() を
を![]() 倍にすると誤差はほぼ
倍にすると誤差はほぼ
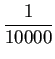 倍になる、
ということである。
倍になる、
ということである。
桂田 祐史