Next: 4.5 複素数 Up: 4 データ Previous: 4.3 整数
Float16, Float32, Float64, BigFloat
(MPFR とか使っている?DD とか QD とかしないのかな?)
BigInt を BigInt で割り算すると、 BigFloat になる。
typeof(BigInt(1)/BigInt(1)) |
BigFloat の精度は setprecision(b) で指定する。
ここで b は2進法での桁数である。
10進法で ![]() 桁欲しければ、
桁欲しければ、
![]() とすればよい。
(
とすればよい。
(
![]() を解いて、
を解いて、
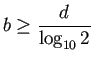 だから、
だから、
![]() 進
進![]() 桁欲しければ
setprecision(Int(ceil(100/log10(2)))) とするのかなと考えたが、
こういうのは余裕を見るべきだから、「
桁欲しければ
setprecision(Int(ceil(100/log10(2)))) とするのかなと考えたが、
こういうのは余裕を見るべきだから、「![]() 倍より多く」で概算すれば良いだろう。
(受験生やった人は
倍より多く」で概算すれば良いだろう。
(受験生やった人は
![]() というのを覚えていそう。)
というのを覚えていそう。)
また sqrt(BigInt(2)) のように、 結果が浮動小数点数になる関数の引数に BigInt 型の値を渡しても、 結果の型は BigFloat になる。
julia> digits=100 julia> Int(ceil(digits/log10(2)))これで 333と出る。 julia> setprecision(333) julia> x=sqrt(BigInt(2)) 1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038753432764157271 julia> x*x 1.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999989 julia> x*x-2 -1.14298739128227498221578354830534095945190999482279866121512584322763263590673819567544802186017202965e-100 |