Next: 4.2 ターゲット問題1 自由落下 Up: 4 2階微分方程式 Previous: 4 2階微分方程式
物理学に疎い人にはピンと来ないかもしれないが、 Newtonの運動方程式が2階の微分方程式である、という話をする。
力学においては、Newton の運動の三法則というのが基本である。
そのうちの第二法則は、Newtonの運動方程式とも呼ばれるもので、
言葉で書くと「質量かける加速度![]() 力」という内容である。
力」という内容である。
質点の運動の場合、時刻 ![]() における質点の位置を
における質点の位置を ![]() で表すと、
加速度は
で表すと、
加速度は
![]() であるから、運動方程式は
であるから、運動方程式は
![]() が既知とすれば、これは2階の微分方程式である。
が既知とすれば、これは2階の微分方程式である。
この後に説明する、2階の微分方程式を1階の微分方程式に書き直す方法が適用できる。 ある意味でフライングになるが、それをやってみよう。
| (34) | 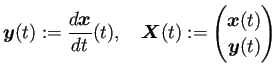 |
![$\displaystyle \frac{\D\bm{X}}{\D t}(t)
=\begin{pmatrix}
\dfrac{\D\bm{x}}{\D t...
...ix} =\begin{pmatrix}
\bm{y}(t) [1ex]
\dfrac{1}{m}\bm{f}(t)
\end{pmatrix}.
$](img143.png)
| (35) | 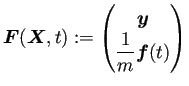 |
| (36) | 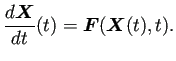 |