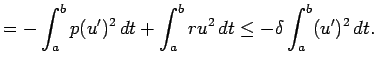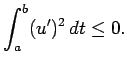ここに書いてある話は良く知られていることではあるが、
(初学者は探すのが一苦労であろうから)
参考書をあげれば、例えば藤田 [2]。
桂田 [3] というノートがある。
[3] で書いたまとめを引用しておく。
| 2階線形常微分方程式の境界値問題のまとめ |
- 正値性の仮定 (
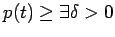 )を満たす )を満たす  階線型
常微分方程式の境界値問題について、
交代定理「可解 階線型
常微分方程式の境界値問題について、
交代定理「可解 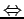 一意 一意 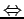 一意可解」がなりたつ。 一意可解」がなりたつ。
- 同次境界条件の場合、
一意可解性が成り立つならば、
境界値問題の解は Green 関数を用いて
表わされる。
- 形式的自己共役な場合には、
一意可解性の簡単で具体的な判定条件がある。
またその場合、Green 関数は対称性を持つ。
- 形式的自己共役でない場合も、
十分小さい (絶対値の大きな負数)
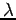 に
対して、 に
対して、
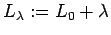 に対する境界値問題の一意可解性が成り立つ。 に対する境界値問題の一意可解性が成り立つ。
|
また明治大学数学科3年生向けの「常微分方程式1」 (by 森本先生) でも講義される。
以下のまとめかたは、その講義の内容を拝借したものである。
直接のつながりはないが、
初期値問題の Green 関数については、
桂田 [4] を見よ。
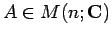 ,
, 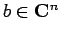 に対して、
に対して、
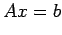 |
(2) |
という線形方程式を考えよう
(未知数の個数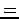 方程式の個数,の連立1次方程式)。
に注意しよう。このとき、任意の
方程式の個数,の連立1次方程式)。
に注意しよう。このとき、任意の 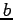 に対して、
(2) の解は一意的に存在し、それは
に対して、
(2) の解は一意的に存在し、それは 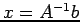 で与えられる。
で与えられる。
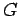 を境界値問題
(3)
の Green関数 (Green function) と呼ぶ。
を境界値問題
(3)
の Green関数 (Green function) と呼ぶ。
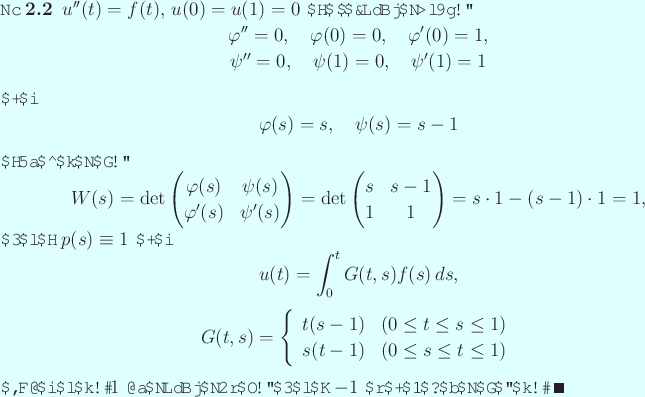
なお、藤田 [2] 定理? では、
という境界条件も扱っている。
任意の 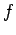 に対して解が存在することから、
一意性が出るか?
に対して解が存在することから、
一意性が出るか?
![$ p,q,r\in C([a,b];\C)$](img54.png) かな?
かな?
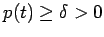 はどこで効くのだろう?
はどこで効くのだろう?
証明.
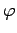
,
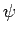
を定める常微分方程式の初期値問題は、
確かに一意可解である。
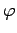 ,
, 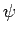 は1次独立である。実際、
は1次独立である。実際、
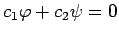 とすると、
とすると、
とおくと、
であるから、一意性の仮定から
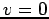
が導かれ、
ゆえに Wronskian は
0 にならない:
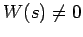
(
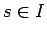
).
後のために、
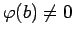 ,
,
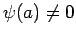 を示す。
もしも
を示す。
もしも
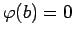 と仮定すると、
と仮定すると、
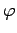 は
は
![$ L_0[\varphi]=0$](img69.png) ,
,
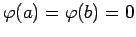 を満たすので、
仮定 (同次境界値問題の解の一意性) から、
を満たすので、
仮定 (同次境界値問題の解の一意性) から、
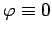 が導かれ、
が導かれ、
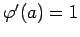 と矛盾する。同様にして
と矛盾する。同様にして
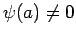 が得られる。
が得られる。
定数変化法で解を求めよう。
とおくと、
ここで
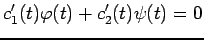 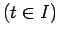 |
(3) |
を仮定すると、
ゆえに
これらから、
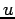
が
![$ L_0[u]=f$](img81.png)
の解であるためには
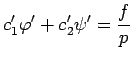 |
(4) |
であることが必要十分である。
(
4), (
5) をまとめて
ゆえに
これから (
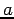
と
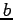
のどちらから積分するかは、後を見越した工夫)
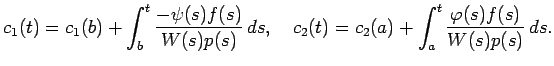 |
(5) |
ゆえに
境界条件に代入して (
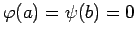
に注意すると)、
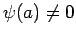
,
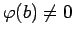
であるから、
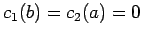
.
ゆえに

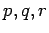 が実数値で、
が実数値で、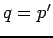 である場合、
である場合、
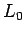 は形式的自己共役であるという
1。
これは
は形式的自己共役であるという
1。
これは
となることにちなむ。実際
に注意すると、
この証明を見れば分かるように、
「形式的自己共役」というときは、境界条件も込めて考えるべきものである
(そういう意味では、
境界条件に言及しない「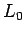 は形式的自己共役」という言い方には問題がある)。
は形式的自己共役」という言い方には問題がある)。
証明.
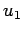
,
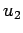
が共に解とする。
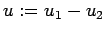
とおく。
が成り立つ。
![$ L_0[u]$](img106.png)
に
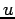
をかけて部分積分すると
移項して
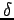
で割って
これから
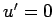
.
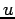
は定数だが、
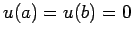
なので実は

.
ゆえに
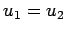
.


証明.
上の二つの定理の系である。


桂田 祐史
![]() ,
, ![]() に対して、
に対して、
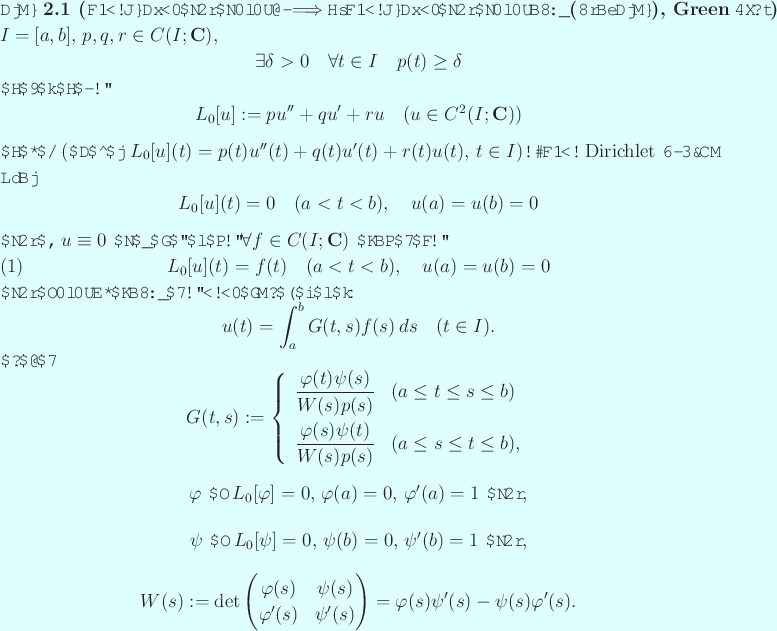
![]() を境界値問題
(3)
の Green関数 (Green function) と呼ぶ。
を境界値問題
(3)
の Green関数 (Green function) と呼ぶ。
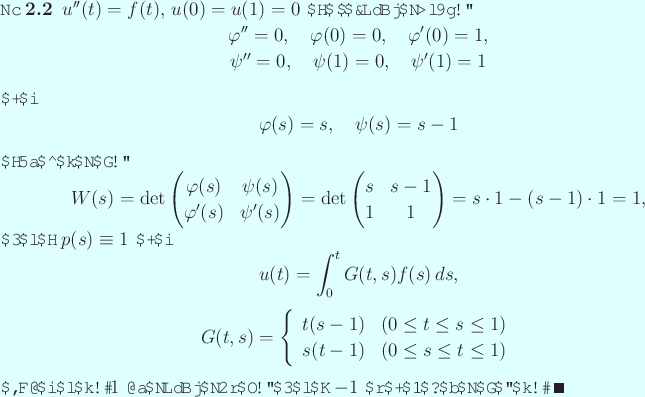
![]() に対して解が存在することから、
一意性が出るか?
に対して解が存在することから、
一意性が出るか?
![]() かな?
かな?
![]() はどこで効くのだろう?
はどこで効くのだろう?
![]() ,
, ![]() は1次独立である。実際、
は1次独立である。実際、
![]() とすると、
とすると、
![]() ,
,
![]() を示す。
もしも
を示す。
もしも
![]() と仮定すると、
と仮定すると、
![]() は
は
![]() ,
,
![]() を満たすので、
仮定 (同次境界値問題の解の一意性) から、
を満たすので、
仮定 (同次境界値問題の解の一意性) から、
![]() が導かれ、
が導かれ、
![]() と矛盾する。同様にして
と矛盾する。同様にして
![]() が得られる。
が得られる。
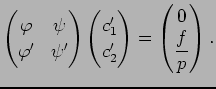
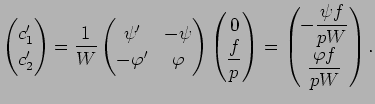
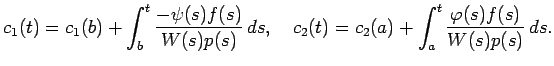
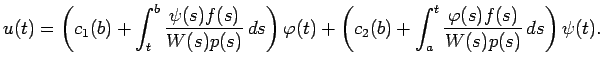
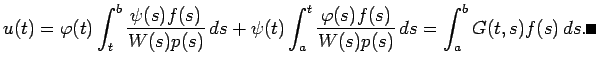
![]() が実数値で、
が実数値で、![]() である場合、
である場合、
![]() は形式的自己共役であるという
1。
これは
は形式的自己共役であるという
1。
これは
![$\displaystyle =\int_a^b(p u')'v \Dt+\int_a^b r uv \Dt =\left[p(t) u'(t) v(t)\right]_a^b -\int_a^b(p u')v' \Dt +\int_a^b r u v \Dt$](img98.png)
![$\displaystyle =-\int_a^b u'(p v')\Dt +\int_a^b r u v \Dt =-\left[u(t)p(t)v'(t)\right]_a^b+\int_a^b u (pv')'\Dt+\int_a^b r u v \Dt$](img99.png)
![$\displaystyle =\int_a^b u\left[(pv')'+rv\right]\Dt =(u,L_0[v]).$](img100.png)
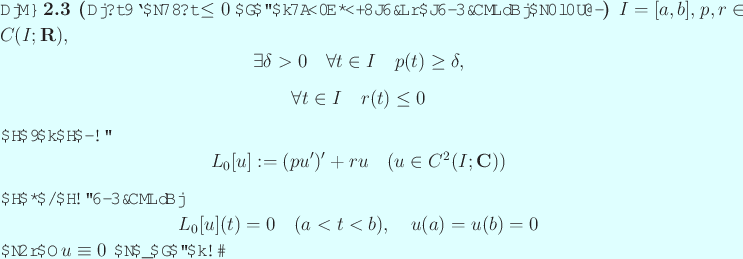
![$\displaystyle =\int_a^b (p u')' u \D t+\int_a^b r u^2 \Dt =\left[p u' u\right]_a^b-\int_a^b p u' u' \Dt+\int_a^b r u^2 \Dt$](img108.png)