Next: A..10 9_Diffusion_1D.c Up: A. 講習会のサンプル・プログラムを読む Previous: A..8 7_Wave_2D_ColorMap.c
| 8_Wave_2D_BirdView.c |
1 /******************************************************************************************
2
3 This program solves a wave equation using the explicit method.
4
5 A wave equation is utt = c * c * uxx.
6 The function f is the initial shape of wave.
7
8 Time loop in this program consists of
9 "Calculation part" and "Draw Part".
10
11 Calculation part is controlled by the interval parameter INTV.
12 This numerical result is visualized by using "g_bird_view_3D" of GLSC3D.
13 Please note that this program set "g_def_scale_3D".
14
15 *******************************************************************************************/
16
17 #include<stdio.h>
18 #include<glsc3d_3.h>
19
20 #define N (100)
21 #define M (100)
22
23 double f(double x,double y)
24 {
25 return 3 * exp(-((x - M_PI / 2)*(x - M_PI / 2) + (y - 3 * M_PI / 2)*(y - 3 * M_PI / 2))/ 0.1);
26 }
27
28 int main()
29 {
30 double x, y;
31
32 double Lx = 8 * M_PI;
33 double Ly = 8 * M_PI;
34 double Lz = 8 * M_PI;
35 double dx = Lx / N;
36 double dy = Ly / M;
37 double dt = 0.002;
38 double c = 1.0;
39
40 double u0[N + 2][M + 2];
41 double u1[N + 2][M + 2];
42 double u2[N + 2][M + 2];
43
44 double lambda_x = c * dt / dx;
45 double lambda_y = c * dt / dy;
46
47 int INTV = 100;
48
49 g_init("Window", 600, 600); //Pixel Size
50
51 g_def_scale_3D_fix(0, //ID
52 -Lx*0.5, Lx*0.5, //xmin,xmax
53 -Ly*0.5, Ly*0.5, //ymin,ymax
54 -Lz*0.5, Lz*0.5, //zmin,zmax
55 20.0, 20.0, //Window (Left, Top) Position
56 560, 560); //Window Size (x,y)
57
58 // g_vision(0, //ID
59 // 0.0, -Ly, Lz, //eye
60 // 0.0, 0.0, 1.0, //up
61 // 1.25 //zoom
62 // );
63 //Set initial calculation
64 {
65 //Step1
66 for(int j = 1;j < M + 1; j ++)
67 {
68 y = (j - 0.5) * dy;
69 for(int i = 1;i < N + 1; i ++)
70 {
71 x = (i - 0.5) * dx;
72 u0[i][j] = f(x,y);
73 }
74 }
75 //Step2
76 for(int j = 1;j < M + 1; j ++)
77 {
78 u0[0][j] = -u0[1][j];
79 u0[N + 1][j] = -u0[N][j];
80 }
81 for(int i = 0;i < N + 2; i ++)
82 {
83 u0[i][0] = -u0[i][1];
84 u0[i][M + 1] = -u0[i][M];
85 }
86 //Step3
87 for(int j = 1;j < M + 1; j ++)
88 {
89 y = (j - 0.5) * dy;
90 for(int i = 1;i < N + 1; i ++)
91 {
92 x = (i - 0.5) * dx;
93 u1[i][j] = u0[i][j] + lambda_x * lambda_x * (u0[i - 1][j] - 2 * u0[i][j] + u0[i + 1][j]) / 2
94 + lambda_y * lambda_y * (u0[i][j - 1] - 2 * u0[i][j] + u0[i][j + 1]) / 2;
95 }
96 }
97 //Step4
98 for(int j = 1;j < M + 1; j ++)
99 {
100 u1[0][j] = -u1[1][j];
101 u1[N + 1][j] = -u1[N][j];
102 }
103 for(int i = 0;i < N + 2; i ++)
104 {
105 u1[i][0] = -u1[i][1];
106 u1[i][M + 1] = -u1[i][M];
107 }
108 }
109
110 //////////// Start time loop ////////////
111 for (int i_time = 0; ; i_time++) {
112
113 //////////// Draw Part ////////////
114 if (i_time%INTV == 0) {
115 g_cls(); //Clear window
116 g_sel_scale(0); //Select Virtual scale
117 g_line_color(0.0, 0.0, 0.0, 1.0);
118 g_boundary(); //Draw Boundary
119
120 g_area_color(1.0, 0.0, 0.0, 1.0);
121 g_bird_view_3D(-Lx*0.5 + dx * 0.5, Lx*0.5 - dx * 0.5, -Ly*0.5 + dy * 0.5, Ly*0.5 - dy * 0.5, N+2, M+2, u0, G_NO, G_YES); //Bird View
122
123 g_finish(); //flush Draw buffer
124 g_sleep(0.01); //Sleep 0.01 sec
125 }
126
127 //////////// Calculation Part ////////////
128 {
129 //Step5
130 for(int j = 1;j < M + 1; j ++)
131 {
132 for(int i = 1;i < N + 1; i ++)
133 {
134 u2[i][j] = 2 * u1[i][j] - u0[i][j]
135 + lambda_x * lambda_x *
136 (u1[i - 1][j] -2 * u1[i][j] + u1[i + 1][j])
137 + lambda_y * lambda_y *
138 (u1[i][j - 1] -2 * u1[i][j] + u1[i][j + 1]);
139 }
140 }
141 //Step5
142 for(int j = 1;j < M + 1; j ++)
143 {
144 for(int i = 1;i < N + 1; i ++)
145 {
146 u0[i][j] = u1[i][j];
147 }
148 }
149 //Step6
150 for(int j = 1;j < M + 1; j ++)
151 {
152 u0[0][j] = -u0[1][j];
153 u0[N + 1][j] = -u0[N][j];
154 }
155 for(int i = 0;i < N + 2; i ++)
156 {
157 u0[i][0] = -u0[i][1];
158 u0[i][M + 1] = -u0[i][M];
159 }
160 //Step7
161 for(int j = 1;j < M + 1; j ++)
162 {
163 for(int i = 1;i < N + 1; i ++)
164 {
165 u1[i][j] = u2[i][j];
166 }
167 }
168 //Step8
169 for(int j = 1;j < M + 1; j ++)
170 {
171 u1[0][j] = -u1[1][j];
172 u1[N + 1][j] = -u1[N][j];
173 }
174 for(int i = 0;i < N + 2; i ++)
175 {
176 u1[i][0] = -u1[i][1];
177 u1[i][M + 1] = -u1[i][M];
178 }
179 }
180 }
181 return 0;
182 }
|
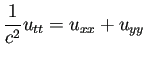 を差分法で解いた解を
のグラフの鳥瞰図 (bird view) を描くプログラム。
を差分法で解いた解を
のグラフの鳥瞰図 (bird view) を描くプログラム。