Next: A..9 8_Wave_2D_BirdView.c Up: A. 講習会のサンプル・プログラムを読む Previous: A..7 6_Turing_2D_ColorMap.c
| 7_Wave_2D_ColorMap.c |
/******************************************************************************************
This program solves a wave equation using the explicit method.
A wave equation is utt = c * c * uxx.
The function f is the initial shape of wave.
Time loop in this program consists of
"Calculation part" and "Draw Part".
Calculation part is controlled by the interval parameter INTV.
This numerical result is visualized by using "g_color_map".
*******************************************************************************************/
#include<stdio.h>
#include<glsc3d_3.h>
#define N (100)
#define M (100)
//////////// Color map: g_color_map ////////////
void g_color_map(double Array[][M+2],
double dx_width, double dy_width,
double L_bottom_x, double L_bottom_y,
double max, double min
)
{
int Fine_Grid = 1;
for (int j=0; j < M+2; j++) {
for (int i=0; i < N+2; i++) {
if (Fine_Grid == 0) {
g_area_color((Array[i][j]-min)/(max-min), 0, 1.0-(Array[i][j]-min)/(max-min), 0.5);
g_box_center_2D(dx_width * (i) + L_bottom_x, dy_width * (j) + L_bottom_y, dx_width, dy_width, G_NO, G_YES);
}
if (Fine_Grid == 1) {
double tmpColor;
if (j-1<0) tmpColor = Array[i][j];
else tmpColor = Array[i][j]*0.5 + Array[i][j-1]*0.5;
g_area_color((tmpColor-min)/(max-min), 0, 1.0-(tmpColor-min)/(max-min), 1);
g_triangle_2D(dx_width * (i) + L_bottom_x, dy_width * (j) + L_bottom_y,
dx_width * (i) + L_bottom_x - dx_width*0.5, dy_width * (j) + L_bottom_y - dy_width*0.5,
dx_width * (i) + L_bottom_x + dx_width*0.5, dy_width * (j) + L_bottom_y - dy_width*0.5,
G_NO, G_YES);
if (i+1>=N+2) tmpColor = Array[i][j];
else tmpColor = Array[i][j]*0.5 + Array[i+1][j]*0.5;
g_area_color((tmpColor-min)/(max-min), 0, 1.0-(tmpColor-min)/(max-min), 1);
g_triangle_2D(dx_width * (i) + L_bottom_x, dy_width * (j) + L_bottom_y,
dx_width * (i) + L_bottom_x + dx_width*0.5, dy_width * (j) + L_bottom_y - dy_width*0.5,
dx_width * (i) + L_bottom_x + dx_width*0.5, dy_width * (j) + L_bottom_y + dy_width*0.5,
G_NO, G_YES);
if (j+1>=M+2) tmpColor = Array[i][j];
else tmpColor = Array[i][j]*0.5 + Array[i][j+1]*0.5;
g_area_color((tmpColor-min)/(max-min), 0, 1.0-(tmpColor-min)/(max-min), 1);
g_triangle_2D(dx_width * (i) + L_bottom_x, dy_width * (j) + L_bottom_y,
dx_width * (i) + L_bottom_x + dx_width*0.5, dy_width * (j) + L_bottom_y + dy_width*0.5,
dx_width * (i) + L_bottom_x - dx_width*0.5, dy_width * (j) + L_bottom_y + dy_width*0.5,
G_NO, G_YES);
if (i-1<0) tmpColor = Array[i][j];
else tmpColor = Array[i][j]*0.5 + Array[i-1][j]*0.5;
g_area_color((tmpColor-min)/(max-min), 0, 1.0-(tmpColor-min)/(max-min), 1);
g_triangle_2D(dx_width * (i) + L_bottom_x, dy_width * (j) + L_bottom_y,
dx_width * (i) + L_bottom_x - dx_width*0.5, dy_width * (j) + L_bottom_y + dy_width*0.5,
dx_width * (i) + L_bottom_x - dx_width*0.5, dy_width * (j) + L_bottom_y - dy_width*0.5,
G_NO, G_YES);
}
}
}
}
double f(double x,double y)
{
return 3 * exp(-((x - M_PI / 2)*(x - M_PI / 2) + (y - 3 * M_PI / 2)*(y - 3 * M_PI / 2))/ 0.1);
}
int main()
{
double x, y;
double Lx = 8 * M_PI;
double Ly = 8 * M_PI;
double dx = Lx / N;
double dy = Ly / M;
double dt = 0.002;
double c = 1.0;
double u0[N + 2][M + 2];
double u1[N + 2][M + 2];
double u2[N + 2][M + 2];
double lambda_x = c * dt / dx;
double lambda_y = c * dt / dy;
int INTV = 100;
g_init("Window", 600, 600); //Pixel Size
g_def_scale_2D(0, //ID
-Lx*0.5, Lx*0.5, //xmin,xmax
-Ly*0.5, Ly*0.5, //ymin,ymax
20.0, 20.0, //Window (Left, Top) Position
560, 560); //Window Size (x,y)
//Set initial calculation
{
//Step1
for(int j = 1;j < M + 1; j ++)
{
y = (j - 0.5) * dy;
for(int i = 1;i < N + 1; i ++)
{
x = (i - 0.5) * dx;
u0[i][j] = f(x,y);
}
}
//Step2
for(int j = 1;j < M + 1; j ++)
{
u0[0][j] = -u0[1][j];
u0[N + 1][j] = -u0[N][j];
}
for(int i = 0;i < N + 2; i ++)
{
u0[i][0] = -u0[i][1];
u0[i][M + 1] = -u0[i][M];
}
//Step3
for(int j = 1;j < M + 1; j ++)
{
y = (j - 0.5) * dy;
for(int i = 1;i < N + 1; i ++)
{
x = (i - 0.5) * dx;
u1[i][j] = u0[i][j] + lambda_x * lambda_x * (u0[i - 1][j] - 2 * u0[i][j] + u0[i + 1][j]) / 2
+ lambda_y * lambda_y * (u0[i][j - 1] - 2 * u0[i][j] + u0[i][j + 1]) / 2;
}
}
//Step4
for(int j = 1;j < M + 1; j ++)
{
u1[0][j] = -u1[1][j];
u1[N + 1][j] = -u1[N][j];
}
for(int i = 0;i < N + 2; i ++)
{
u1[i][0] = -u1[i][1];
u1[i][M + 1] = -u1[i][M];
}
}
//////////// Start time loop ////////////
for (int i_time = 0; ; i_time++) {
//////////// Draw Part ////////////
if (i_time%INTV == 0) {
g_cls(); //Clear window
g_sel_scale(0); //Select Virtual scale
g_line_color(0.0, 0.0, 0.0, 1.0);
g_boundary(); //Draw Boundary
g_color_map(u0, dx, dy, -Lx*0.5 + dx * 0.5, -Ly*0.5 + dy * 0.5, 0.2, -0.2);
g_finish(); //flush Draw buffer
g_sleep(0.01); //Sleep 0.01 sec
}
//////////// Calculation Part ////////////
{
//Step5
for(int j = 1;j < M + 1; j ++)
{
for(int i = 1;i < N + 1; i ++)
{
u2[i][j] = 2 * u1[i][j] - u0[i][j]
+ lambda_x * lambda_x *
(u1[i - 1][j] -2 * u1[i][j] + u1[i + 1][j])
+ lambda_y * lambda_y *
(u1[i][j - 1] -2 * u1[i][j] + u1[i][j + 1]);
}
}
//Step6
for(int j = 1;j < M + 1; j ++)
{
for(int i = 1;i < N + 1; i ++)
{
u0[i][j] = u1[i][j];
}
}
//Step7
for(int j = 1;j < M + 1; j ++)
{
u0[0][j] = -u0[1][j];
u0[N + 1][j] = -u0[N][j];
}
for(int i = 0;i < N + 2; i ++)
{
u0[i][0] = -u0[i][1];
u0[i][M + 1] = -u0[i][M];
}
//Step8
for(int j = 1;j < M + 1; j ++)
{
for(int i = 1;i < N + 1; i ++)
{
u1[i][j] = u2[i][j];
}
}
//Step9
for(int j = 1;j < M + 1; j ++)
{
u1[0][j] = -u1[1][j];
u1[N + 1][j] = -u1[N][j];
}
for(int i = 0;i < N + 2; i ++)
{
u1[i][0] = -u1[i][1];
u1[i][M + 1] = -u1[i][M];
}
}
//////////// Check part of maximum and minimum of u and v in order to use g_color_map ////////////
// double u_Max = u0[0][0];
// double u_Min = u0[0][0];
// for(int j = 1;j < M + 1; j ++)
// {
// for(int i = 1;i < N + 1; i ++)
// {
// if (u_Max < u0[i][j]) u_Max = u0[i][j];
// if (u_Min > u0[i][j]) u_Min = u0[i][j];
// }
// }
// printf("%d th: u_Max = % 2.15f\n", i_time, u_Max);
// printf("%d th: u_Min = % 2.15f\n", i_time, u_Min);
}
return 0;
}
|
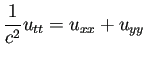 を差分法で解いた解を
値を色で表して可視化するプログラム。
を差分法で解いた解を
値を色で表して可視化するプログラム。