

Next: 2.3 が正定値である場合にその Cholesky 分解を用いる方法
Up: 2 標準固有値問題への帰着
Previous: 2.1 問題点
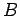 が正則な場合、
が正則な場合、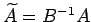 とおくと、
とおくと、
となる。
そこで 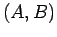 の一般化固有値
の一般化固有値 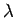 の (代数的) 重複度を
の (代数的) 重複度を
の重複度によって定義する2。
これから 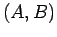 の一般化固有値も重複度を考えてちょうど
の一般化固有値も重複度を考えてちょうど 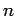 個だけ
存在することが分かる。
個だけ
存在することが分かる。
![\begin{jremark}[計算向きの方法ではない]
$A$, $B$ が対称であっ...
...模な問題でない限り問題外であろう\footnotemark )。
\end{jremark}](img29.png)


Next: 2.3 が正定値である場合にその Cholesky 分解を用いる方法
Up: 2 標準固有値問題への帰着
Previous: 2.1 問題点
桂田 祐史
2014-05-27
![]() が正則な場合、
が正則な場合、![]() とおくと、
とおくと、
![\begin{jproposition}[$B$ が正則な場合]
$A$, $B$ は $n$ 次正方行�...
...�し $I$ は $n$ 次単位行列である。
\end{enumerate}\end{jproposition}](img25.png)
![]() の一般化固有値
の一般化固有値 ![]() の (代数的) 重複度を
の (代数的) 重複度を