Next: A. プログラム Up: 単振り子の話 Previous: 3 単振動との比較
振幅が ![]() である単振り子の周期は
(
である単振り子の周期は
(![]() が 0
から
が 0
から ![]() に変化するのに要する時間の
に変化するのに要する時間の![]() 倍だから)
倍だから)
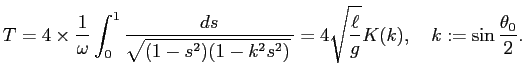
ただし
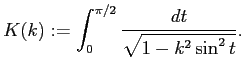
これと単振動の周期
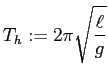
との比
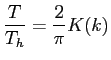
を具体的に計算してみよう。
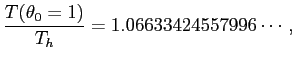
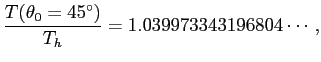
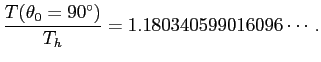
つまり
![$\displaystyle K(k)=\frac{\pi}{2}
\left[1+\left(\frac{1}{2}\right)^2k^2
+\left...
...k^4
+\left(\frac{1\cdot3\cdot5}{2\cdot 4\cdot6}\right)^2k^6
+\cdots
\right]
$](img88.png)
であるから
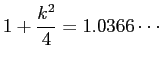 . あまり良い近似でないかな?
(もう1項くらい取れば…)。
. あまり良い近似でないかな?
(もう1項くらい取れば…)。
| 0 | 1.000000000000000 |
| 10 | 1.001907188143217 |
| 20 | 1.007669025791545 |
| 30 | 1.017408797595956 |
| 40 | 1.031340519130037 |
| 50 | 1.049782960623032 |
| 60 | 1.073182007149365 |
| 70 | 1.102144909639270 |
| 80 | 1.137492559923922 |
| 90 | 1.180340599016096 |
| 100 | 1.232229196737520 |
| 110 | 1.295339998876550 |
| 120 | 1.372880500618350 |
| 130 | 1.469819325894477 |
| 140 | 1.594446101177228 |
| 150 | 1.762203729503756 |
| 160 | 2.007507401244124 |
| 170 | 2.439362719673885 |
| 179 | 3.901065160389150 |
図 5 は、
これをグラフにしたものである。
![]() はあまり現実的な振り子の運動と言えないから、
はあまり現実的な振り子の運動と言えないから、
![]() の場合のみ注目すると、
振り子の等時性はほどほどの精度で成立する、と言えそうである。
の場合のみ注目すると、
振り子の等時性はほどほどの精度で成立する、と言えそうである。
(振り子の等時性が成り立たないことは実験してみれば分かる、 という人がいるけれど、 かなり真剣に取り組まないとはっきりしないのではないか? と思う。)
桂田 祐史