Next: 2 微分方程式の解析 Up: 単振り子の話 Previous: 単振り子の話
紐の長さが ![]() である単振り子
(たんしんし単振子, simple pendulum) の運動方程式は、
である単振り子
(たんしんし単振子, simple pendulum) の運動方程式は、
![]() を重りの質量、
を重りの質量、![]() を重力加速度として
を重力加速度として
となる。これから
微小振動 (
![]() ) の場合は、
) の場合は、
![]() は
は ![]() に近いので、
単振り子の運動は
に近いので、
単振り子の運動は
に従う単振動で良く近似できる、とされる (高校物理の相場)。 単振動は (大学の理系の学科では) 「常識的」で1、一般解は
であり、これは周期
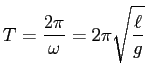
を持つ周期関数である、と明解に解ける。 この周期が
しかし、単振動で近似するのはあくまでも近似である。 どうして近似を用いた説明が多いのかというと、 近似しないで解くのが難しいからである (後で見るように、解や周期を表すのに、 楕円関数、楕円積分というものが必要になる2)。 この文書の目的は、 本来の振り子の運動 (微分方程式 (1) の解) がどうなるか (近似を用いずに)、きちんと考えてみよう、 ということである。
単振り子は、 単振動ではないとすると、 本当に周期運動をするか?と心配となるが、 次節でも証明するエネルギー保存則
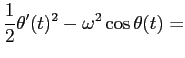 定数
定数
より大丈夫であることが分かる (戻ってきた時、前と同じ速さであり、減衰したりはしない 3。
ガリレオが発見したという『振り子の等時性』は、 実は厳密には成立しない性質であるが (つまり周期は本当は振幅による)、 どの程度成り立っているものなのかも、 明らかにしよう (目で見て分かるようにする -- 後の図 5)。
桂田 祐史