Next: A. ごみ箱 Up: 7. 双対空間についてのメモ Previous: 7.3 埋め込まれた空間の双対
![]() 内の可測集合
内の可測集合 ![]() ,
,
![]() に
対して Lebesgue 空間
に
対して Lebesgue 空間
![]() を考える。
以下
を考える。
以下 ![]() は固定するので、
は固定するので、
![]() のことを単に
のことを単に ![]() と書く。
と書く。
よくある習慣にのっとり、
![]() に対して、
に対して、
![]() を共役指数とする。
すなわち
を共役指数とする。
すなわち
![]() ならば
ならば ![]() は
は
![]() となる数、
となる数、
![]() ならば
ならば ![]() ,
, ![]() ならば
ならば 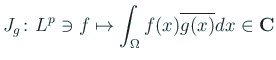 .
.
任意の
![]() ,
,
![]() に対して、
に対して、
とおくと、
から分かる。
こうして
という写像が定義されるが、これは等距離写像である。すなわち
実は
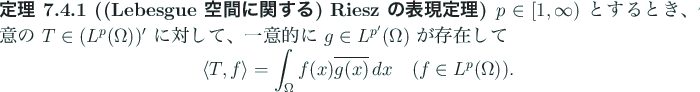 の場合、この写像
の場合、この写像
![]() は
全射 (従って Banach 空間の同型写像) であることが、
次の Riesz の表現定理から保証される。
は
全射 (従って Banach 空間の同型写像) であることが、
次の Riesz の表現定理から保証される。
|
|
この事実を ![]() を省略して単に
を省略して単に
![]() (
(
![]() ) と書
くことが多い。
) と書
くことが多い。
![]() のときは
のときは ![]() は全射にはならない。すなわち
は全射にはならない。すなわち
![]() は Banach 空間であり、
は Banach 空間であり、![]() は等長であるから、
は等長であるから、
![]() は
は
![]() の閉部分空間である (特に
の閉部分空間である (特に
![]() は
は
![]() で稠密ではない)。
だから
で稠密ではない)。
だから
![]() は
は ![]() よりもかなり大きい (感覚的な話)。
よりもかなり大きい (感覚的な話)。
桂田 祐史