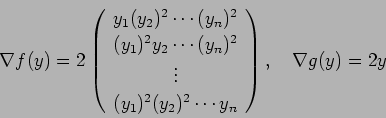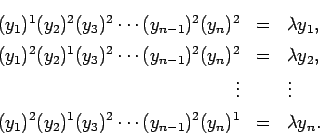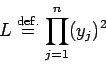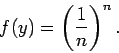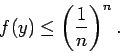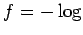 гБ®гБКгБПгБ®
гБ®гБКгБПгБ® 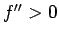 гБІгБВгВЛгБУгБ®гБЂж≥®жДПгБЩгВМгБ∞гАБ
еЙНе∞ПзѓАгБЃеСљй°МгВИгВКжШОгВЙгБЛгАВ
гБІгБВгВЛгБУгБ®гБЂж≥®жДПгБЩгВМгБ∞гАБ
еЙНе∞ПзѓАгБЃеСљй°МгВИгВКжШОгВЙгБЛгАВ
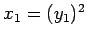 ,
, 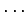 ,
, 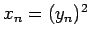 гБ®гБКгБПгБУгБ®гБЂгВИгВКгАБ
гБ®гБКгБПгБУгБ®гБЂгВИгВКгАБ
гВТи®ЉжШОгБЩгВМгБ∞гВИгБДгБМгАБеРМжђ°жАІгБЛгВЙеНШдљНзРГйЭҐдЄКгБІ
гВТз§ЇгБЫгБ∞еНБеИЖгБІгБВгВЛгАВ
гБЭгБУгБІ
гБ®гБКгБНгАБжЭ°дїґ 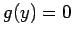 гБЃгВВгБ®гБІгБЃ
гБЃгВВгБ®гБІгБЃ 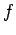 гБЃжЬАе§ІеА§гВТи™њгБєгВЛгАВ
гБЊгБЪжЦєз®ЛеЉП
гБЃжЬАе§ІеА§гВТи™њгБєгВЛгАВ
гБЊгБЪжЦєз®ЛеЉП 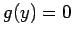 гБѓеНШдљНзРГйЭҐгВТи°®гВПгБЧгАБгБУгВМгБѓгВ≥гГ≥гГСгВѓгГИгБІгБВгВЛгБЛгВЙгАБ
жЬАе§ІеА§гБМе≠ШеЬ®гБЩгВЛгБУгБ®гБМеИЖгБЛгВЛгАВ
гБЊгБЯ
гБѓеНШдљНзРГйЭҐгВТи°®гВПгБЧгАБгБУгВМгБѓгВ≥гГ≥гГСгВѓгГИгБІгБВгВЛгБЛгВЙгАБ
жЬАе§ІеА§гБМе≠ШеЬ®гБЩгВЛгБУгБ®гБМеИЖгБЛгВЛгАВ
гБЊгБЯ
гБІгБВгВЛгБЛгВЙгАБжЭ°дїґ 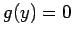 гБЃгВВгБ®гБІгБѓ
гБЃгВВгБ®гБІгБѓ
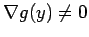 . гВЖгБИгБЂ
жЬАе§ІеА§гБѓењЕгБЪ Lagrange гБЃжЬ™еЃЪдєЧжХ∞ж≥ХгБІж±ВгБЊгВЛгАВгБ§гБЊгВКжЬАе§ІеА§зВє
. гВЖгБИгБЂ
жЬАе§ІеА§гБѓењЕгБЪ Lagrange гБЃжЬ™еЃЪдєЧжХ∞ж≥ХгБІж±ВгБЊгВЛгАВгБ§гБЊгВКжЬАе§ІеА§зВє 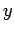 гБІгБѓ
гБІгБѓ
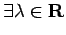 s.t.
s.t.
гБУгВМгВТжИРеИЖгБІжЫЄгБПгБ®
жШОгВЙгБЛгБЂжЬАе§ІеА§гБѓж≠£гБІгБВгВЛгБЛгВЙгАБ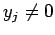 (
(
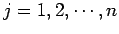 ).
гВЖгБИгБЂ
).
гВЖгБИгБЂ
гБ®гБКгБПгБ®гАБ
гБУгВМгБЛгВЙ
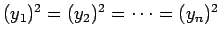 . еТМгБМ
. еТМгБМ 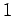 гБІгБВгВЛ
(
гБІгБВгВЛ
(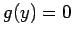 ) гБЛгВЙгАБ
) гБЛгВЙгАБ
гВЖгБИгБЂжЭ°дїґ 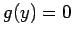 гБЃдЄЛгБІгБЃ
гБЃдЄЛгБІгБЃ 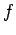 гБЃжЬАе§ІеА§гБѓ
гБЃжЬАе§ІеА§гБѓ
гБУгВМгБЛгВЙ 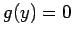 гВТжЇАгБЯгБЩдїїжДПгБЃ
гВТжЇАгБЯгБЩдїїжДПгБЃ 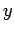 гБЂеѓЊгБЧгБ¶гАБ
гБЂеѓЊгБЧгБ¶гАБ
гВЖгБИгБЂ
ж°ВзФ∞ з•РеП≤
2017-04-30