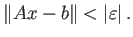Next: 13 convect() Up: 12 弱形式を定義して解く Previous: 12.1 solve, problem
solve, problem を使ってプログラムを書くと、
連立1次方程式 ![]() が「見えない」けれど、以下のようにして
varf を用いると係数行列
が「見えない」けれど、以下のようにして
varf を用いると係数行列 ![]() 、右辺の既知ベクトル
、右辺の既知ベクトル ![]() が得られる。
そうするのがお勧めなのだそうだ。
が得られる。
そうするのがお勧めなのだそうだ。
(おまけ: この辺の説明を読んでいて、 ようやく固有値問題を解くコード https://doc.freefem.org/models/eigen-value-problems.htmlが理解出来るようになった。)
| poisson3.edp |
// poisson3.edp
// Freefem++ poisson3.edp
border C(t=0,2*pi) {x=cos(t); y=sin(t);}
mesh Th = buildmesh(C(50));
fespace Vh(Th,P1);
Vh u,v;
func f=x*y;
varf a(u,v)= int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v)) + on(C,u=0);
matrix A=a(Vh,Vh);
varf L(unused,v) = int2d(Th)(f*v) + on(C,unused=0);
Vh F; F[] = L(0,Vh);
u[]=A^-1*F[];
plot(u);
|
このプログラムでは F は Vh の元としたが、 次のように配列にしても良い。
real [int] F=L(0,Vh); u[] = A^-1 * F; |
もう1つ例をあげておく。 説明が前後してしまうが、 18 のプログラム poisson-kikuchi.edp を、 matrix を利用するように書き直してみる。
| poisson-kikuchi-matrix.edp |
// poisson-kikuchi.edp
// https://m-katsurada.sakura.ne.jp/program/fem/poisson-kikuchi.edp
// 菊地文雄, 有限要素法概説, サイエンス社
int Gamma1=1, Gamma2=2;
border Gamma10(t=0,1) { x=0; y=1-t; label=Gamma1; }
border Gamma11(t=0,1) { x=t; y=0; label=Gamma1; }
border Gamma20(t=0,1) { x=1; y=t; label=Gamma2; }
border Gamma21(t=0,1) { x=1-t; y=1; label=Gamma2; }
int m=10;
mesh Th = buildmesh(Gamma10(m)+Gamma11(m)+Gamma20(m)+Gamma21(m));
plot(Th,wait=true,ps="Th.eps");
savemesh(Th,"Th.msh");
fespace Vh(Th,P1);
Vh u,v;
func f=1;
func g1=0;
func g2=0;
varf a(u,v)=int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v)) + on(Gamma1,u=g1);
matrix A=a(Vh,Vh);
varf L(unused,v)=-int2d(Th)(f*v)-int1d(Th,Gamma2)(g2*v);
Vh F;
F[] = L(0,Vh);
u[]=A^-1*F[];
plot(u,wait=1,ps="poisson-kikuchi.eps");
//3次元鳥瞰図
//real [int] levels =0.0:0.01:1.0;
//plot(u,dim=3,viso=levels,fill=true,wait=true);
|
実際にどういう連立1次方程式を解いているのか、のぞくことが出来て便利である。
連立1次方程式のソルバーを指定するには solver=名前 を用いる
(problem Poisson(u,v,solver=LU) =... とか
matrixA=a(Vh,Vh,solver=CG,eps=1e-10) のように指定する)。
使用可能なソルバーとしては、次のようなものがある、
とのことであるが、普通は UMFPACK を使う
(これがデフォールトである)
のだそうだ。
どういうように使い分けるのかは、良く知らない
(個々の用語は良く使われるものなので、一応は意味が分かるのだけれど、
実際にどういう条件の下でどちらを選ぶかの判断が出来ない)。
| solver= | 対象とする行列 | |
| UMFPACK | multi-frontal LU | 疎 |
| CG | CG法 | 疎, 正値対称 |
| LU | skyline, 非対称 | |
| Crout | Crout法 | skyline, 対称 |
| Cholesky | Cholesky法 | skyline, 対称, 正値 |
| GMRES | GMRES法 | 疎 |
| sparsesolver | 疎 |
反復法における停止則は、eps=![]() で指定する。
で指定する。
![]() のときは
のときは