5.2 Liouvilleの定理, Abelの定理

$\begin{jproposition}[Liouvilleの第1定理] (全平面で)正則な楕円関数は定数関数に等しい。 \end{jproposition}$

証明. 二重周期性から、値域は、基本領域 (あるいはその閉包) の像に等しく、それはコンパクトであるから有界である。ゆえに、「有界な整関数は定数関数に限る」と言うLiouvilleの定理から、定数関数であることが導かれる。 $\qedsymbol$ $\qedsymbol$

$\begin{jproposition}[Liouvilleの第2定理] 楕円関数 $f$ の任意の1つ�... ...a$ に属する $f$ の極の留数の和は$0$である。 \end{jproposition}$

証明.

の極は孤立しているので、 $\Delta$ を平行移動した $\Delta'$ の周上に極がないように出来る。

の周期性から、 $\Delta$ に属する極における留数の和と、 $\Delta'$ に属する極における留数の和は等しいので、 $\Delta'$ について留数の和が 0 であることを示せば良い。ゆえに最初から $\Delta$ の周上に極がないとして示せば良い。

$\Delta$ の周に沿って正の向きに一周する閉曲線 $\rd\Delta$ に沿う線積分は、周期性から0に等しい。留数定理によって、その $\Delta$ 内部の留数の和は0に等しい。 $\qedsymbol$ $\qedsymbol$

$\begin{jdefinition}[楕円関数の位数] 楕円関数$f$の、任意の1つ�... ...るとき、$f$ は$m$位の楕円関数であるという。 \end{jdefinition}$
(基本領域の選び方によらずに定まることに注意せよ。)

$\begin{jcorollary} $1$位の楕円関数は存在しない。 \end{jcorollary}$

証明.

位の楕円関数

が存在したとする。

は、ただ1つの極を持ち、その位数は

であるが、その留数は命題5.11 によって0である。これは、それが

の極であることに矛盾する。 $\qedsymbol$ $\qedsymbol$

$\begin{jproposition}[Liouvilleの第3定理] 楕円関数 $f$ の1つの基本�... ...極の位数の和と、零点の位数の和は等しい。 \end{jproposition}$

証明. $\Delta$ の周上に

の極、零点が存在しないとして示せば良い。

を楕円関数とする。の周期はの周期でもあり $\dfrac{f'}{f}$ の周期でもある。 $\Delta$ の周を正の向きに一周する閉曲線 $\rd\Delta$ について、偏角の原理から

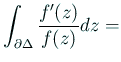$\displaystyle \int_{\rd\Delta}\frac{f'(z)}{f(z)}\Dz =$ 零点の位数の和 $\displaystyle -$ 極の位数の和 $\displaystyle .$

この線積分の値は命題5.11 で見たように0であるから、

零点の位数の和 $\displaystyle =$ 極の位数の和 $\displaystyle . \qed$

$\qedsymbol$

$\begin{jproposition}[Abelの定理 (Liouvilleの第4定理)] 位数が2以上�... ...aymath} ただし $\Gamma$ は $f$ の周期群である。 \end{jproposition}$