![]() の列ベクトルを
の列ベクトルを
![]() ,
, ![]() ,
,
![]() とする:
とする:
| (5) |
この
![]() ,
, ![]() ,
,
![]() に Gram-Schmidt の
直交化法を施して
に Gram-Schmidt の
直交化法を施して
![]() ,
, ![]() ,
,
![]() を作る。
つまり
を作る。
つまり
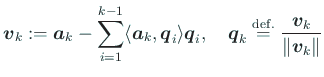
として計算するわけだが4、 中間変数
| (6) | 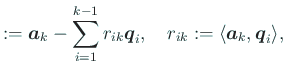 | |
| (7) | 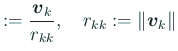 |
さて
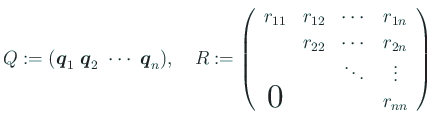
とおくと、
ここまで ![]() は複素行列として計算してきたが、実行列である場合は、
は複素行列として計算してきたが、実行列である場合は、
![]() ,
, ![]() も実行列 (したがって
も実行列 (したがって ![]() は実直交行列) である。
は実直交行列) である。
![\begin{jdefinition}[QR 分解]\upshape
正則行列 $A\in GL(n;\C)$\ に対し�...
...�出すことを $A$\ を \textbf{QR 分解}すると言う。
\end{jdefinition}](img292.gif)
|
上の議論から任意の正則行列は QR 分解可能であることが分かったが、実はこ れは一意的である。
|
|
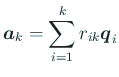
と書ける。
から
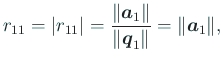
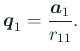
次に
から、まず
これから
は計算できて、
であるから、
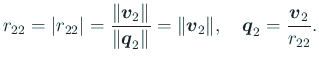
以下