Next: B..2 変形 Bessel 関数 Up: B. おもちゃ箱 Previous: B. おもちゃ箱
離心近点角 ![]() ,
平均近点角
,
平均近点角 ![]() , 楕円の離心率
, 楕円の離心率
![]() について
について
が成り立つが、これを Kepler の方程式と呼ぶ。 この解は Bessel 関数を用いて
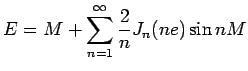
と解ける。
(![]() と
と ![]() が与えられて
が与えられて ![]() を
求めるには、ということだろうけれど、
数値的に求めるだけならば、
直接方程式を Newton 法で解くのが早いだろうな。
まあ、パラメーター依存性とか見るにはよいのだろうけれど。)
を
求めるには、ということだろうけれど、
数値的に求めるだけならば、
直接方程式を Newton 法で解くのが早いだろうな。
まあ、パラメーター依存性とか見るにはよいのだろうけれど。)
|
(書きかけ)
楕円軌道
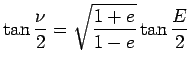
を解けば良い。 |

桂田 祐史