Next: 5.2 有理関数の積分への応用 Up: 5 数値積分の高橋・森による誤差解析理論 Previous: 5 数値積分の高橋・森による誤差解析理論
(準備中 -- 「数値積分ノート」[1] の付録 G にある。)
![]() ,
,
![]() は
は
![]() における
における
![]() の開近傍
の開近傍 ![]() で定義された
正則関数とするとき
で定義された
正則関数とするとき
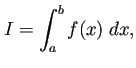
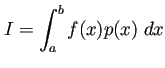
多くの数値積分公式は、
![]() と
と
![]() を用いて
を用いて
簡単のため、以下では ![]() ,
, ![]() が有限と仮定する。
が有限と仮定する。
![]() は
は ![]() 内の区分的に
内の区分的に![]() 級の閉曲線で、
級の閉曲線で、
![]() を正の向きに一周しているとする。
を正の向きに一周しているとする。
![]() とするとき、Cauchy の積分公式から
とするとき、Cauchy の積分公式から
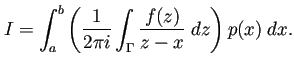
積分順序の交換が容易に出来て、
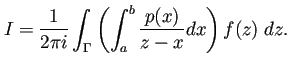
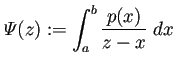 |
(34) |
![]() は
は ![]() の Hilbert 変換と呼ばれ、
の Hilbert 変換と呼ばれ、
![]() で正則である (証明は容易)。
で正則である (証明は容易)。
![]() の場合は
の場合は
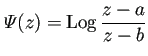
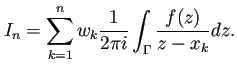
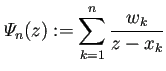 |
(36) |
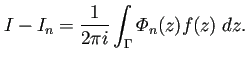
大まかに言うと、
![]() が小さいならば、
数値積分の誤差の大きさ
が小さいならば、
数値積分の誤差の大きさ
![]() が小さいと期待できる。
数値積分公式の良し悪しが
が小さいと期待できる。
数値積分公式の良し悪しが ![]() を調べることで判定できる。
を調べることで判定できる。
実際、講義で説明したような数値積分公式に対して、
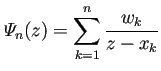 は、
は、
![]() の有理関数近似となっていることが示される (詳しいことは…)。
の有理関数近似となっていることが示される (詳しいことは…)。
高橋・森は、誤差の特性関数を上のように定義して、
![]() 内の
内の ![]() を含む領域で
を含む領域で
![]() を図示して、
研究した。
を図示して、
研究した。
桂田 祐史