2006年度の金子君は、 参考に出来るものがほとんどない状態で一定の成果をあげたが、 見通しのよいものでなかったので、 久保田君はまずはそこを整理するところから始める必要があった。 決して大きな一歩とは言えないが、着実な前進が出来たと評価したい。
問題とする領域 ![]() に対して、
に対して、
と仮定し、
条件
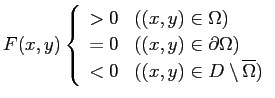
を満たす関数
また 4つの関数
![]() ,
,
![]() ,
,
![]() ,
,
![]() を次のように定義する
(東西南北 (east-west-south-north) から命名したのだろう)。
を次のように定義する
(東西南北 (east-west-south-north) から命名したのだろう)。
(数学的には、条件を満たす ![]() が1つ与えられれば、
が1つ与えられれば、
![]() ,
, ![]() ,
, ![]() ,
, ![]() は決まってしまうわけだが、
具体的にどう計算するかは決して自明でないので、
プログラム中で別途与えることにしたわけである。)
は決まってしまうわけだが、
具体的にどう計算するかは決して自明でないので、
プログラム中で別途与えることにしたわけである。)
-- こうして、ほぼ F(), E(), W(), S(), N() と いう5つの関数を用意するだけで、 新しい問題が解けるようになるのは非常に面白いのみならず、 実用面でも大きな期待が持てるものである。 特にトポロジーが長方形領域と異なる領域の問題を解くプログラムがすいすい書 けるのは、正直新鮮な驚きであった。
レポートは http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2007-kubota.pdfで、プログラムも http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2007-kubota-prog.lzhで公開中である。