一様な棒が振動するとき、変位 ![]() は、適当な単位を選択した場合、
微分方程式
は、適当な単位を選択した場合、
微分方程式
に従う。 この方程式の初期値境界値問題の研究をテーマとした。 これは波動方程式に少し似ていて、 有名な Cournat-Hilbert にも取り上げられている。
境界条件としては次のいずれかを考える。
| (1) |
| (2) |
| (3) |
これらは「対称性の条件」を満たしていることが分かる。例えば、
![]() が固定境界条件
が固定境界条件
を満たしているのならば、
が成り立つ。ここで微分作用素
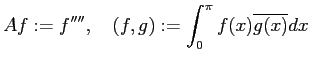
で定義されるものとする。 これから、固有値が実数であることと、 異なる固有関数に属する固有関数が互いに直交することが分かる。
(a) の場合の固有値は、方程式
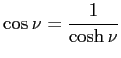
の正の解である。それを大きさの順に
と並べたとき、
である。
(b) の場合の固有値は ![]() (
(![]() ) であり、それに属する固有関数は
) であり、それに属する固有関数は
である。
(c) の場合の固有値は、方程式
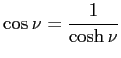
の正の解である。それを大きさの順に
と並べたとき、