plot xの式 とすると、
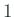 変数関数のグラフが描ける2。
変数関数のグラフが描ける2。
描いたものは clear コマンドで消せるが、
plot コマンドを使うと古い図は消えるので、
あまり使う必要はないかもしれない。
式をカンマで区切って複数書くことで、複数のグラフを重ねて描ける。
| gnuplot> plot sin(x),cos(x) |
|
|
変数 (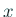 座標) の範囲を指定することができる。
座標) の範囲を指定することができる。
| gnuplot> plot [-pi:pi] sin(x),cos(x) |
|
|
あるいは事前に
| gnuplot> set xrange [-pi:pi] |
|
|
のように指定しておくこともできる
(unset xrange でクリアできる)。
ここで pi という組み込みの定数を用いた。
| おまけ: pi について確認 |
| gnuplot> print pi |
← print コマンドで式の値が表示できる |
| 3.14159265358979 |
→ 確かに円周率 |
|
複雑な式の関数を何度も使う場合は、
関数定義をしておくと便利である。
| gnuplot> f(x)=x**3-3*x**2+4*x-5 |
←
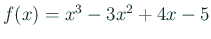 を定義 を定義 |
| gnuplot> plot f(x) |
|
|
| gnuplot> f(x)=exp(-x*x/2)/sqrt(2*pi) |
← 標準正規分布の確率密度関数を定義 |
| gnuplot> plot [-3:3] f(x) |
|
|
図 1:
正規分布の確率密度関数 (
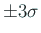 の範囲)
の範囲)
|
![\includegraphics[width=7cm]{normal.eps}](img24.gif) |
値 (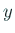 座標) の範囲も指定することができる。
座標) の範囲も指定することができる。
| gnuplot> plot [-pi/2:pi/2] [-10:10] tan(x) |
← 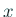 , , 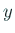 両方とも指定 両方とも指定 |
| gnuplot> plot [] [-10:10] tan(x) |
← 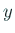 座標のみ指定 座標のみ指定 |
|
簡単な場合分けは、C言語風の三項演算子 ? で実現できる。
| gnuplot> f(x)=(abs(x)<1)? (x**2-1)**4:0 |
← 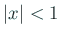 で で 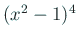 , それ以外で 0 , それ以外で 0 |
| gnuplot> plot [-2:2] [-0.1:1.1] f(x) |
|
|
変化が激しい関数の場合、関数値を計算する点の個数を
(デフォールトの 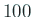 から)
増やす必要がある。
から)
増やす必要がある。
| gnuplot> plot sin(100*x) |
|
| gnuplot> set samples 10000 |
|
| gnuplot> plot sin(100*x) |
|
|
replot というコマンドがある。
画面に表示して確認したものをファイルに保存する目的で、
再描画するために使われることが多いが(後述する)、
重ね書きする目的で使うこともできる。
| gnuplot> plot [-1:1] x**2 |
|
| gnuplot> replot x**3 |
|
| gnuplot> replot x**4 |
|
|
同じことは (上で説明したように) , で区切って並べても良い。
| gnuplot> plot [-1:1] x**2,x**3,x**4 |
|
|
この場合は for による繰り返しを使っても実現できる。
| gnuplot> plot [-1:1] for [i=2:4] x**i |
|
|
さらに for の少し凝った使い方
(title を用いた凡例指定の中で繰り返しの変数を用いる)。
| gnuplot> plot for [i=1:10] 0.2*i*exp(x) title sprintf("%.1f*exp(x)", i*0.2) |
|
|
(sprintf() は C 言語で同じもの書式指定で文字列を作る関数である
(説明略)。)
桂田 祐史
![]() 変数関数のグラフが描ける2。
変数関数のグラフが描ける2。
![]() 座標) の範囲を指定することができる。
座標) の範囲を指定することができる。
![]() 座標) の範囲も指定することができる。
座標) の範囲も指定することができる。
![]() から)
増やす必要がある。
から)
増やす必要がある。