Next: 23 gdb を使えるようにする Up: 2018年のコンピューターノウハウ (Mac) Previous: 21 PDF 形式の図のクロップ
(しばらく工事中)
以前のメモは
の第2節にある。
久しぶりに exflib を使ってみる。 動機は、これまた久しぶりに MATLAB を使うために色々見直していて、 それならば前から気になっていた MATLAB から exflib を使う、 というのを試してみよう、ということである。
まず g++, gfortran 向けの exflib
(MATLAB 用とは独立なので、MATLAB で使うだけならば、必要はないけれど。)
Mac用の最新版は、
あ、以前と違って .pkg ではないのか。
curl -O http://www-an.acs.i.kyoto-u.ac.jp/~fujiwara/exflib/exflib-x64-bin-20180620.tar.bz2 tar xjf exflib-x64-bin-20180620.tar.bz2 cd exflib-x64-bin-20180620 ls less README.txt |
cd sample-cxx make |
(Makefile をちょっと修正)
% diff Makefile Makefile.org 33,34c33 < #PROG=fact napier pi zero function test complex taylor contfrac matrix version subnormal < PROG=fact napier pi zero test complex taylor contfrac matrix version subnormal --- > PROG=fact napier pi zero function test complex taylor contfrac matrix version subnormal % make(無事終了) |
出来上がった実行形式を起動すると、 一応動いているみたいだけれど、 どうなったら正しく動いているのか、すぐ分かるようになっていない。 「ソースを読め」ということらしい。 作者が動かした環境での結果くらいを含めておいてくれると楽なのだけど。
ライブラリィ・アーカイブ・ファイルとインクルード・ファイルを システムのディレクトリィにコピーして、 それを使ってコンパイルしてみる。
sudo cp -p ../exflib-x86_64-intelmac/libexfloat.a /usr/local/lib sudo cp -p ../exflib-x86_64-intelmac/*.h /usr/local/include g++ -Wall -O2 -m64 -I/usr/local/include -o napier napier.cpp -lexfloat ./napier |
2.718282e+0 2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427 2.718281828459045235360287471352662497757247093699959574966967627724076630353547594571382178525166427 |
exflib を使うプログラムをコンパイルするには、 次の2点に注意する。
まとめると
| こうするとインストールできるはず |
curl -O http://www-an.acs.i.kyoto-u.ac.jp/~fujiwara/exflib/exflib-x64-bin-20180620.tar.bz2 tar xjf exflib-x64-bin-20180620.tar.bz2 sudo cp -p exflib-x64-bin-20180620/exflib-x86_64-intelmac/libexfloat.a /usr/local/lib sudo cp -p exflib-x64-bin-20180620/exflib-x86_64-intelmac/*.h /usr/local/include |
プログラムの書き方については、 ずっと以前 「多倍長計算ノート」 の第2節に少し書いておいた。
では MATLAB 向けの exflib
| ターミナルで |
curl -O http://www-an.acs.i.kyoto-u.ac.jp/~fujiwara/exflib/exflib-MATLAB-20180902-distribute.zip unzip exflib-MATLAB-20180902-distribute.zip cd exflib-MATLAB-20180902-distribute ls cat README.txt cd .. |
MATLAB を起動して、実行してみる。
| MATLABで |
>> cd ${SOMEWHERE}/exflib-MATLAB-20180902-distribute
>> ls
>> edit fact
>> fact
|
これも一体どうなるべきものなのか、説明がない。
使うたびに cd したり、PATH を気にしたくないので、 設定しようと考えたのだけど、どうすべきか、説明が書かれてない。 自分でやんなさい、ということかな。
動くための条件は次の2つらしい。
結局次のようにした。 まず、
cd ~/Documents/MATLAB
cp -pr ${SOMEWHERE}/exflib-MATLAB-20180902-distribute/exflib .
cp -pr ${SOMEWHERE}/exflib-MATLAB-20180902-distribute/@exfloat exflib
|
addpath('~/Documents/MATLAB/exflib');
|
以上をまとめると
| こうするとインストール&設定出来るはず (その1) |
curl -O http://www-an.acs.i.kyoto-u.ac.jp/~fujiwara/exflib/exflib-MATLAB-20180902-distribute.zip
unzip exflib-MATLAB-20180902-distribute.zip
cp -pr exflib-MATLAB-20180902-distribute/exflib ~/Documents/MATLAB
cp -pr exflib-MATLAB-20180902-distribute/@exfloat ~/Documents/MATLAB/exflib
echo "addpath('~/Documents/MATLAB/exflib')">> ~/Documents/MATLAB/startup.m
|
実は exflib-MATLAB-20180902-distribute の下に、 いくつか .m ファイルがあるので、 それも見えるようにしようと考えると、
| こうするとインストール&設定出来るはず (その2) |
curl -O http://www-an.acs.i.kyoto-u.ac.jp/~fujiwara/exflib/exflib-MATLAB-20180902-distribute.zip
unzip exflib-MATLAB-20180902-distribute.zip
mv exflib-MATLAB-20180902-distribute ~/Documents/MATLAB/exflib-20180902
echo "addpath('~/Documents/MATLAB/exflib-20180902')">>~/Documents/MATLAB/startup.m
echo "addpath('~/Documents/MATLAB/exflib-20180902/exflib')">>~/Documents/MATLAB/startup.m
|
ともあれ、テスト。
まず ![]() を計算してみよう。
を計算してみよう。
| MATLABのコマンド・ウィンドウで |
f=exfloat(1);
for n=1:100
f=f*n;
fprintf('fact %d = %s\n', n, num2str(f, '%f'));
end
|
精度は動的には変化させられず、@exfloat/exfloat.m で指定する。
| exfloat.m の最初の8行 |
classdef exfloat
properties (Constant, Access=private)
%----------------------------------------
% required precision in decimal digits
%----------------------------------------
precision10 = 500;
|
線型差分方程式 (符号に注意2)
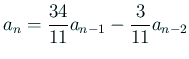 |
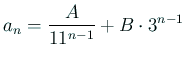 (
(
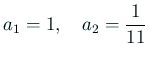
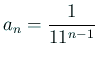 である。
である。
clear classes;
a(1)=exfloat(1);
a(2)=exfloat('1/11');
for n=3:50
a(n)=exfloat('34/11')*a(n-1)-exfloat('3/11')*a(n-2);
end
plot(a)
figure semilogy(a) |
exfloat の代わりに普通の double では
clear('a')
a(1)=1;
a(2)=1/11;
for n=3:50
a(n)=34/11 * a(n-1)-3/11*a(n-2);
end
plot(a)
figure
semilogy(a)
|
ここでは片側対数目盛りのグラフのみ載せておく。
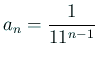 であるから、
まっすぐ右下がりの直線となるべきものである。
double で計算した場合は、
であるから、
まっすぐ右下がりの直線となるべきものである。
double で計算した場合は、
桂田 祐史