Next: 5 計算練習: の Fourier 係数 Up: 4 計算練習: の Fourier 係数 Previous: 4 計算練習: の Fourier 係数
Mathematica で Fourier 係数を求めるには、 上に紹介した FourierCosCoefficient[], FourierSinCoefficient[] を使うのが便利であるが、 基本的な機能を用いて計算するどうなるか、少し見ておこう。
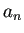 が求まる? が求まる? |
1/Pi Integrate[f[x]Cos[n x],{x,-Pi,Pi}]
|
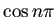 ,
, 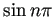 というのが出て来る。
というのが出て来る。
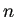 が整数と仮定していないので、簡単にならない。
が整数と仮定していないので、簡単にならない。
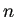 が
が
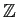 (the set of all integers) の要素 (element) であることを
Element[n,Integers] と教えてみよう。
(the set of all integers) の要素 (element) であることを
Element[n,Integers] と教えてみよう。
a[n_]:=Simplify[1/Pi Integrate[f[x]Cos[n x],{x,-Pi,Pi}],Element[n,Integers]]
a[n]
|
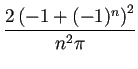 が得られる。
この結果は
が得られる。
この結果は 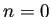 のときナンセンスである。
その場合は別に計算しなければいけないのは、手計算と同じであるが、
遅延評価をする := を使って関数定義してあるので、単に
のときナンセンスである。
その場合は別に計算しなければいけないのは、手計算と同じであるが、
遅延評価をする := を使って関数定義してあるので、単に
a[0] |
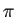 が得られる。
が得られる。
Table[a[n],{n,0,10}]
|