Next: B..3.3 MATLABプログラム Up: B..3 2次元の場合 (結果だけ紹介) Previous: B..3.1 差分方程式
簡単のため、同次 Dirichlet 境界条件 (
![]() ) の場合に説明する。
) の場合に説明する。
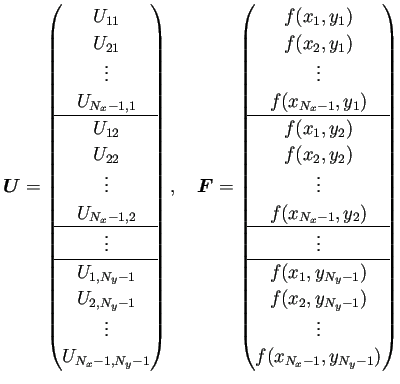

プログラムを書くときのために、![]() ,
, ![]() の成分
の成分
![]() ,
, ![]() を式で表しておく。
を式で表しておく。
| (B.17) | ||
| (B.18) |
![[*]](crossref.png) ) の代わりに
) の代わりに
![[*]](crossref.png) ) を row first,
(
) を row first,
(![[*]](crossref.png) ) を column first と呼んで区別する。
次に紹介する MATLAB プログラムでは、
(
) を column first と呼んで区別する。
次に紹介する MATLAB プログラムでは、
(![[*]](crossref.png) ) を採用してある。
) を採用してある。