Next: 3.3.1 サンプル・プログラム Up: 3 有限要素法と FreeFem++ Previous: 3.2 FreeFem++ プログラム (その2)
(2022/8/12 追記。2023年度の授業で用いるため。しばらく工事中。 内容の正しさは保証しない。)
流れ関数をどのように求めるか。Jordan領域であれば、 境界上の流れ関数の値が
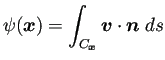
ところで、もしも境界上で ![]() が既知ならば、
実は Neumann 境界データ
が既知ならば、
実は Neumann 境界データ
![]() も求められる。
も求められる。
![]() である。
である。
速度ポテンシャルと同様にして流れ関数が求められることになる。 以上は実はこれまで気づいていなかった (ちょっと恥ずかしい)。 まだ忙しくて整理する時間がないが、散逸するとまずいので、 とりあえず書いたメモをここに移しておく。
どちらかというと「複素関数と流体力学」に書くことかな?
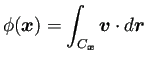
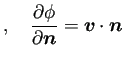 (on
(on

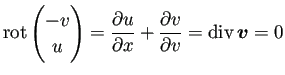
|
(
|
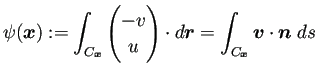 |
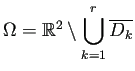 となっていて、各境界
となっていて、各境界
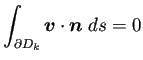
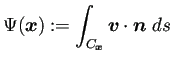
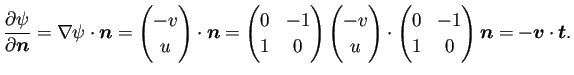
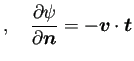 on
on
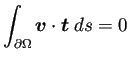
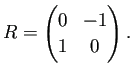
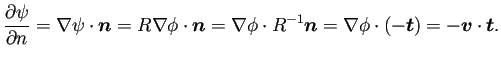
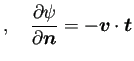 on
on