2.10 比留間 勇人「複合台形公式による留数の数値計算」

正則関数 $f$ の 孤立特異点 $c$ の周りの留数 $\Res(f;c)$ は、 非常に便利な概念であることが複素関数でおなじみであるが、 積分表示

$$\Res(f;c)=\frac{1}{2\pi i}\int_{\vert z-c\vert=\eps} f(z)\;\Dz$$

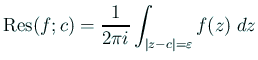
を台形公式で近似計算することにより、容易かつ高精度に数値計算できる。

ある意味では「常識から明らか」かもしれないが (もっとも複素関数と、 「周期的解析関数の周期区間における積分は台形則で高精度に計算できる」 という数値計算に関する知識をどちらもきちんと知っている人は案外少ないかも)、 それを実際の数値計算で試して、その応用を探ってみよう、というテーマである。