1.2 今日すること

大きく分けて次の2つ。どちらも、これからしばらくの課題の説明。

• Mathematica の説明 (題材は Fourier 級数の部分和の可視化)
  (動作チェックを含む)
• 輪講のテキストの方が一段落したら (p. 128の問題まで済んだら) 「発展系の数値解析」 をテキストとして数値実験

細かく分けると以下のようになる。

1. Mathematica で Fourier級数のグラフを描く。
   • 次回までに全員ができるようにすること (サンプル・プログラムを少し変えるだけなので難しくない)。
   • 誰か(「信号処理とフーリエ変換」を履修した人？) に説明してもらう。

以下の課題の質問は随時受け付けるけれど、 次回 (10/30) にそのための時間を取る予定 (ということは11/13からということになりそう)。

1. http://nalab.mind.meiji.ac.jp/~mk/program/fdm/heat1d-e.cを解読して説明する。
   誰かに担当してもらう (「はじめての応用解析」で該当部分(p. 122のあたり)を担当する人？)。
2. 「発展系の数値解析」の4「数値実験例」, 5「陰解法」を読んで、 表や図を再現しながら説明する。
   次回までには担当を決めること。

   (i)

   (1)「解析解との比較」
   表1, 図2を再現すること。

   (ii)

   (2) 「解の漸近挙動」
   グラフと表2を再現すること。

   (iii)

   (3) 「熱伝導方程式の平滑化作用, $t\to\infty$の漸近形」

3. 「発展系の数値解析」の4「陰解法」(2) 後退Euler法
   　グラフも再現すること。
4. 「発展系の数値解析」の4「陰解法」(3) 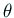$\theta$法, クランク・ニコルソン法
   (46) 式が導かれることをていねいに説明する。
5. http://nalab.mind.meiji.ac.jp/~mk/program/fdm/heat1d-i.c(陰解法プログラム, 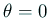$\theta=0$ とすると陽解法) を解読して説明する。
   trilu(), trisol() についての説明は飛ばして良い。
6. 以下の中から出来るものをピックアップ。
   • 補足 (4) 「連立1次方程式が解けること」
   • 補足 (6) 「Gaussの消去法のアルゴリズム」
   • heat1d-i.c の中のtrilu(), trisol() を説明する。
   • Neumann境界条件の場合のプログラム http://nalab.mind.meiji.ac.jp/~mk/program/fdm/heat1n-i.cを説明する。アルゴリズムは、 「長方形に対する差分法」 (http://nalab.mind.meiji.ac.jp/~mk/labo/text/heat-fdm-1.pdf) の§1.3が参考になる。
   • 「発展系の数値解析」の補足 (5) 差分解の厳密解への収束の証明