Next: 2.3.2 プログラムの解読 Up: 2.3 プログラムの解説 Previous: 2.3 プログラムの解説
質点の質量は ![]() とする。
質点の位置は (
とする。
質点の位置は (![]() 成分は考えないことにして)
成分は考えないことにして) ![]() ,
, ![]() 座標で定まる。
そこで
座標で定まる。
そこで
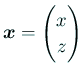
とおく。
質点に働く力は、重力と空気抵抗のみとする。
重力は ![]() (
(
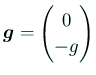 ).
).
空気抵抗は速さに比例した大きさで、速度と逆向きと仮定すると、
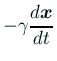 (
(![]() は正の定数) とおける。
は正の定数) とおける。
運動方程式は
| (1) | 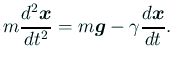 |
| (2) | 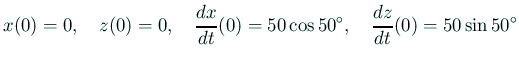 |
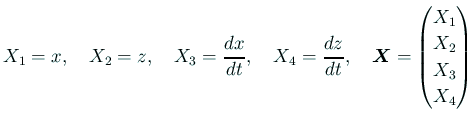
とおくと、
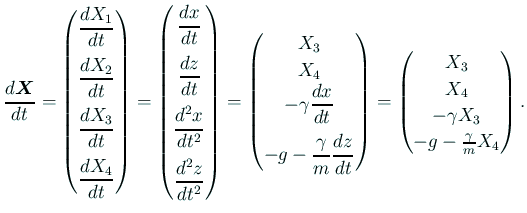
そこで
| (3) | 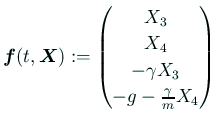 |
| (4) | 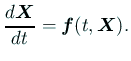 |
| (5) | 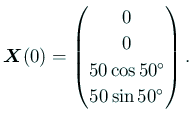 |
桂田 祐史