8.4 Manipulate[]

(工事中)

熱方程式の基本解

$$G(x,t)=\frac{1}{\sqrt{4\pi t}}\exp\left(-\frac{x^2}{4t}\right)$$

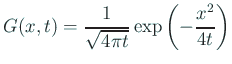
について、$t$ を固定するごとに $x\mapsto G(x,t)$ のグラフを描いてみる。

G[x_, t_] := Exp[-x^2/(4 t)]/(2*Sqrt[Pi*t])
g=Plot[Table[G[x, t], {t, 0.1, 1.0, 0.1}], {x, -5, 5}, PlotRange -> All]
Manipulate[Plot[G[x, t], {x, -5, 5}, PlotRange -> {0, 3}], {t, 0.01, 2}]

図 24: 一度に全部描いてしまうと分かりにくい…

離心率が $e$ の円錐曲線は適当な座標系で

$$r=\frac{1}{1+e\cos\theta}$$

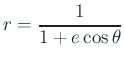
と表すことが出来る。

Manipulate[g=PolarPlot[1/(1 + eps Cos[t]), {t, 0, 2 Pi}], {eps, 0, 2, 0.01}]

図 25: $e=0.65$ は楕円