| n=2^2^5+1 |
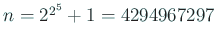
|
| |
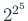 は
は
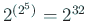 という意味です (
という意味です (
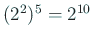 ではない)。
ではない)。 |
| PrimeQ[n] |
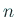 は素数かどうか判定する
は素数かどうか判定する |
| |
素数は英語で prime という。`Q' は Question の頭文字。 |
| EvenQ[n] |
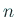 は偶数かどうか判定する
は偶数かどうか判定する |
| |
偶数は英語で even number という。 |
| OddQ[n] |
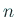 は奇数かどうか判定する
は奇数かどうか判定する |
| |
偶数は英語で odd number という。 |
| FactorInteger[n] |
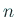 の素因数分解
の素因数分解 |
| 641 6700417 |
掛け算してみる |
| Remove[n] |
おそうじ |
| Mod[123456,123] |
123456 を 123 で割った余り |
| GCD[96,18] |
最大公約数 |
| Table[Prime[n],{n,100}] |
最初の100個の素数 |
| Divisors[48] |
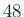 の約数全体
の約数全体 |
|