E. 行列の固有値問題の験算

(某月某日) 「対称行列

$$A=\begin{pmatrix} 0 & 1 & 1 \\ 1 & 0 & -1 \\ 1 & -1 & 0 \end{pmatrix}$$

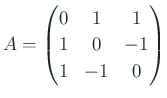
を実直交行列によって対角化せよ」という問題の答えの験算をする。

行列を入力して確認する。

a={{0, 1, 1}, {1, 0, -1}, {1, -1, 0}}
MatrixForm[a]

固有値を求める。 Eigenvalues[] を使えば一発で求まるが、 特性多項式も計算しておこう。

Eigenvalues[a]

f[x_]:=Det[x IdentityMatrix[3] -a]
f[x]

Solve[f[x]==0,x]

固有値は $-2$ , $1$ (重根) であることが分かる。

固有ベクトルは

{v1,v2,v3}=Eigenvectors[a]

これで

$$\bm{v}_1=\begin{pmatrix}-1 1 1 \end{pmatrix},\quad \bm{v}_... ... 0 1 \end{pmatrix},\quad \bm{v}_3=\begin{pmatrix}1 1 0 \end{pmatrix}$$

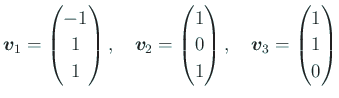
が求まるが、念のために固有値がそれぞれ $-2$ , $1$ , $1$ であることを確認する。

a.v1

a.v1-(-2)v1

a.v2-1 v2

a.v3-1 v3

後の3個のベクトルはいずれも$\bm{0}$ .

Gram-Schmidt の直交化法によって正規直交基底を求める。

u1=v1/Norm[v1]

u2=v2/Norm[v2]

$\bm{v}_2$ は(異なる固有値に属する固有ベクトルなので) $\bm{v}_1$ とは直交しているので、単に正規化すれば良い。 $\bm{v}_3$ からは $\bm{v}_2$ 成分を削除してから正規化する必要がある。

$$\bm{v}_3'=\bm{v}_3-(\bm{v}_3,\bm{u}_2)\bm{u}_2,$$

$$\bm{u}_3=\frac{1}{\left\Vert\bm{v}_3'\right\Vert}\bm{v}_3'$$

とするわけである。

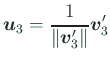vv3=v3-v3.u2 u2
v2.vv3
u3=vv3/Nomr[vv3]

$$\bm{u}_1= \begin{pmatrix} -\frac{1}{\sqrt{3}}\\ \frac{1}{\sqr... ...c{1}{\sqrt{6}}\\ \sqrt{\frac{2}{3}} \\ -\frac{1}{\sqrt{6}} \end{pmatrix}.$$

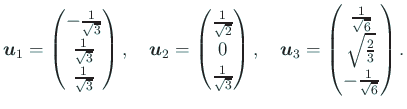
これを並べた行列 $U$ を作って表示し、 $U^T A U$ を計算して固有値が対角線に並んだ対角行列になっていることを確認する。

u=Transpose[{u1,u2,u3}]
MatrixForm[u]

d=Simplify[Transpose[u].a.u]
MatrixForm[d]

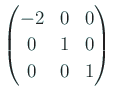結果は無事 $\begin{pmatrix}-2 & 0 & 0 \\ 0 & 1 & 0 0 & 0 & 1 \end{pmatrix}$ になった。