5.21 微分方程式を解く DSolve[], NDSolve[]

(ただ今工事中です。現在の Mathematica は、一部の偏微分方程式や、 境界値問題も解けるようになっていますが、 ここでは常微分方程式やその初期値問題の解き方のみ紹介します。 2019/11/3 LaTeX2HTML が '' を二重引用符 ” に することがあって、コードが壊れていたのを直す。)

常微分方程式を解くコマンド DSolve[] があります。

一つの使い方は、次のように y[x] について解くというものです。

DSolve[y'[x]==a y[x],y[x],x]

結果は {{y[x]->Exp[a x]C[1]}} となります。 つまり

$$\frac{\Dy}{\Dx}=a y$$

の一般解は $y=C_1 e^{ax}$ である、ということですね。 ここから何かするには、演算子 /. を使うことになるでしょう。

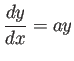
次の例では、単振動の方程式の初期値問題

$$x''(t)=-x(t),\quad x(0)=1,\quad x'(0)=2$$

を解いています。任意定数は残っていないので、結果をグラフで表示できます。 (少々強引に) 関数 x を上書き定義してから、 もう一度グラフを描いています。

Remove[x,t]
sol=DSolve[{x''[t]==-x[t], x[0]==1, x'[0]==2},x[t],t]
Plot[x[t] /. sol, {t,-10,10}]	← グラフを描く (分かり辛い？)
x[t_]:=Evaluate[x[t] /. sol[[1]]]	← 関数 x を定義
	Evaluate[] を使うのが一つのポイント
Plot[x[t], {t,-10,10}]	← グラフを描く (分かりやすい？)

連立の微分方程式を解くことも出来ます。

$$x'(t)=-y(t),\quad y'(t)=2x(t),\quad x(0)=1,\quad y(0)=2$$

という問題は次のようにして解けます。

Remove[t,x,y]
sol=DSolve[{x'[t] == -y[t], y'[t]==2x[t], x[0]==1, y[0]==2},{x[t],y[t]},t]
ParametricPlot[{x[t],y[t]}/.sol,{t,0,2Pi}]

もう一つのやり方は、 y[x] でなく、y について解くと言うものです。 結果は (説明は省略しますが) 「純関数」 {{y->Function[{x},2Exp[a x]]}}になります。 つまり y に /. したときに、 y[] という関数が出来るだけでなく、 y'[x] や y[1] などの式が使えるのが嬉しい点です。

Remove[a,x,y]
sol=DSolve[{y'[x]==a y[x],y[0]==2},y,x]
y[x] /. sol	← この段階では差がない
y'[x]-a y[x] /. sol	← こういうことが出来る(解であることの確かめ)

こちらでも初期値問題が解けます。

Remove[t,x,x0,v0]
s=DSolve[{x''[t] == - omega^2 x[t], x[0] == x0, x'[0] == v0},x,t]

微分方程式は、 いわゆる式変形では解けない場合が多いことは良く知られています。 そのため数値的に近似解を求める方法が色々と開発されています。 NDSolve[] は数値的に微分方程式の初期値問題を解くコマンドで、 結果は離散的な点での関数値を近似的に求めたものになります。 計算していない点での値は補間により簡略計算することになります (こういうものを、 Mathematica では InterpolatingFunction (直訳すると補間関数？) と呼んでいるようです)。

次の例では、いわゆる単振り子の方程式

$$\theta''(t)=-\sin\theta(t)$$

を解いています。良く知られているように(?)、 この解の表示には楕円関数などを使う必要があり (http://nalab.mind.meiji.ac.jp/~mk/labo/text/furiko/ とか)、 ちょっと難しめのせいか、Mathematica も DSolve[] では解いてくれません。 そこで NDSolve[] の出番となります。

振り子の方程式を解く (1)

Remove[t,x]
sol=NDSolve[{x''[t]==-Sin[x[t]],x[0]==1,x'[0]==0}, x, {t,0,10}]
Plot[x[t] /. sol, {t,0,10}]

以前は Plot[Evaluate[x[t] /. sol], {t,0,10}] とかする必要があったのですが、 今では Evaluate[] は不要になったようです。 ただし、オンライン・ヘルプには Evaluate[] するように書いてあるし、 今でも NDSolve[] とプロットを同時にやる場合には、 Evaluate[] した方が無駄なく効率的に計算できます (逆に言うと、そうでない場合の処理は昔と変わったのかな？)。 そこら辺が気になるならば、 Timing[] で時間の計測をして比較すると良いでしょう。

連立1階の方程式

$$x'=y(t),\quad y'(t)=-\sin x(t)$$

に直して解いてみる。

振り子の方程式を解く (2)

Remove[t,x,y]
sol=NDSolve[{x'[t]==y[t], y'[t]==-Sin[x[t]],x[0]==1,y[0]==0}, {x,y}, {t,0,10}]
ParametricPlot[{x[t],y[t]}/.sol, {t,0,10}]

おまけ (未整理)

Remove[t,x,y,t2]
Manipulate[
 ParametricPlot[Evaluate[{x[t2], y[t2]} /. 
   NDSolve[{x'[t] == y[t], y'[t] == -Sin[x[t]], x[0] == x0, 
     y[0] == 0}, {x, y}, {t, 0, 20}]], {t2, 0, 20}, 
  PlotRange -> {{-1.2 Pi, 1.2 Pi}, {-Pi, Pi}}], {x0, 0, Pi}]

とか

Remove[t,x,y,x0,t2,a]
my[x0_] := 
 ParametricPlot[Evaluate[{x[t2], y[t2]} /. 
   NDSolve[{x'[t] == y[t], y'[t] == -Sin[x[t]], x[0] == x0, 
     y[0] == 0}, {x, y}, {t, 0, 20}]], {t2, 0, 20}, 
  PlotRange -> {{-1.2 Pi, 1.2 Pi}, {-Pi, Pi}}]
Show[Table[my[a Pi], {a, 0.1, 0.9, 0.1}]]

とか

Remove[t,x,y,a,b]
sol = Table[{x[t], y[t]} /.
       NDSolve[{x'[t] == y[t], y'[t] == -Sin[x[t]], x[0]==a*Pi, y[0]==b},
        {x, y}, {t, -20, 20}], {b, -2.4, 2.4, 0.2}, {a, -2, 2, 2}];
g = ParametricPlot[sol, {t, -20, 20}, PlotRange -> {{-3 Pi, 3 Pi}, {-Pi, Pi}}]

ちなみにエネルギー保存則の式で描くと

ContourPlot[
 1/2 y^2 - 9.8 Cos[x] - 9.8, {x, -2 Pi, 2 Pi}, {y, -10, 10}, 
 Contours -> Table[x, {x, -40, 40, 5}], AspectRatio -> 0.5]

図 9: 振り子の運動の相図: $\theta (0)=0.1\pi ,\cdots ,0.9\pi$, $\theta '(0)=0$ (そっと手放す)

図 10: 良く本に載っている図

おまけ2: 放物運動

?? Global`*

Remove["Global`*"]

v=20;
theta=45;
ParametricPlot[Evaluate[{x[t2], y[t2]} /.
  NDSolve[{x' '[t] == 0, y' '[t] == -9.8,
    x[0]==0, y[0]==0, x'[0]==v*Cos[theta Degree], y'[0]==v*Sin[theta Degree]},
     {x, y}, {t, 0, 5}]],
   {t2, 0, 4}]

もちろん

DSolve[{x' '[t] == 0, y' '[t] == -g, 
  x[0] == 0, y[0] == 0, x'[0] == v Cos[theta], y'[0] == v Sin[theta]},
  {x, y}, t]

として、式変形で解くことも出来る。