

Next: A. 201x年7月某日のSNS
Up: 情報処理2 第11回 Mathematica 体験
Previous: 2 Mathematica 体験 (前回の続き)
- Oh-o! Meiji を使ってレポートを提出せよ。
形式は、PDF ファイル (kadai11.pdf) で、
締切は 7 月19日(金曜) 18:00 です
(最初 7 月16日(火曜) 18:00 としましたが、延長します)。
次のいずれかを選択して下さい。
- (1)
- 授業などで現れた問題や例を、Mathematica を使って計算してみる。
教科書、授業のノート、プリント、
自分が読んだ本 (授業と全然関係無くても良い) などから、
自分でやるのは大変そうな計算や、グラフ描画など、
適当な問題を探しておいて下さい。
(桂田が作った資料は、
担当している講義科目との関係で,
微積分や、関数論、偏微分方程式よりの例が多くなっているので、
そうでない線形代数や幾何関係の問題がやり甲斐のある問題となるかもしれません。)
- (2)
- Mathemaitca が計算できない、
あるいは間違えた結果を答えるような問題を見つけたら、
その理由を分析して、どの辺に限界があるか確めてみる。
諸君の先輩のレポート例:
高木貞治『解析概論』にある収束する広義積分
を、Mathematica が発散すると答える (もちろん Mathematica の間違い)
ことを発見した。
-- もしかして?と思って最新の Mathmatica 9 で試してみても,
「…の積分は
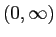 で収束しません」と応答が返ってきました。
で収束しません」と応答が返ってきました。
- (3)
- 3次元空間のラプラシアン
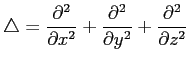 の極座標表示を
Mathematica を使って計算せよ
(微分法の合成関数の微分法の少し面倒気味の計算問題)。
の極座標表示を
Mathematica を使って計算せよ
(微分法の合成関数の微分法の少し面倒気味の計算問題)。
- (4)
- http://nalab.mind.meiji.ac.jp/~mk/syori2/mo/about-Mathematica-for-students/(このページは明治大学内からしか読めません)
を参考に、自宅のパソコンに Mathematica をインストールしてみる。
その過程を報告する。


Next: A. 201x年7月某日のSNS
Up: 情報処理2 第11回 Mathematica 体験
Previous: 2 Mathematica 体験 (前回の続き)
桂田 祐史
2013-07-10
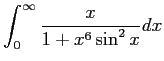
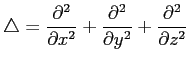 の極座標表示を
Mathematica を使って計算せよ
(微分法の合成関数の微分法の少し面倒気味の計算問題)。
の極座標表示を
Mathematica を使って計算せよ
(微分法の合成関数の微分法の少し面倒気味の計算問題)。