これもレポートを提出するかどうか任意(余裕がある人向けの「挑戦課題」)。 締め切りはこの講義の最終回まで。 提出方法は、 syori2@math.meiji.ac.jp (@はASCIIの@) に電子メールを送ること。
微積分の教科書を見ると、
多くの初等関数
(![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() など)
の Taylor 展開が載っていますが、
など)
の Taylor 展開が載っていますが、
![]() の Taylor 展開が載っている本はあまりありません。
実は
の Taylor 展開が載っている本はあまりありません。
実は ![]() の Taylor 展開の一般項の係数は、
大学2年生が知っているものを使って表すことは出来ません
(ベルヌーイBernoulli 数というものを使うと表示できます)。
しかし、Taylor 展開の最初の数項を求めるだけならば、
大学1,2年生レベルの数学で十分です (素朴で良ければ、
の Taylor 展開の一般項の係数は、
大学2年生が知っているものを使って表すことは出来ません
(ベルヌーイBernoulli 数というものを使うと表示できます)。
しかし、Taylor 展開の最初の数項を求めるだけならば、
大学1,2年生レベルの数学で十分です (素朴で良ければ、
![]() を微分して
を微分して
![]() を求めていけば OK --
でもこれを十進 BASIC で実行するのは至難の技)。
ここでは『関数論1』で学ぶ事項を利用して計算する方法を考えてみます。
を求めていけば OK --
でもこれを十進 BASIC で実行するのは至難の技)。
ここでは『関数論1』で学ぶ事項を利用して計算する方法を考えてみます。
![]() ,
, ![]() は
は ![]() 全体で正則で、
全体で正則で、
![]() (
(![]() ) であるから、
) であるから、
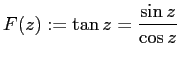
は
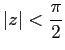 で正則であり、
で正則であり、
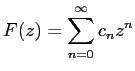
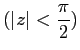
と Taylor 展開が出来るはずである。 これを求める (
![\begin{jlemma}[冪級数の割り算]
一般に、$0$ の近傍における
収...
..._{n-k}}{a_0}\quad\mbox{($n\in\N$)}
\end{equation}が成り立つ。
\end{jlemma}](img98.png)
|
すなわち
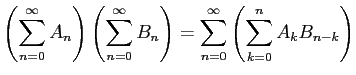
から、
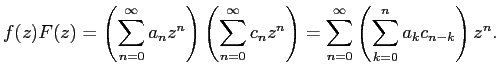
これが
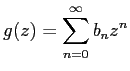 と等しいので、
係数を比較して、
と等しいので、
係数を比較して、
 | ||
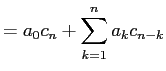 |
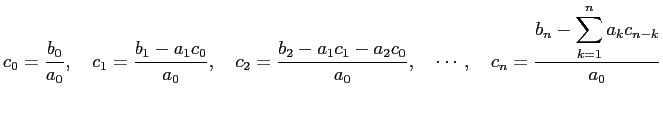
次の問に答えよ。
上の公式 (1) と、
![]() ,
, ![]() の 0
のまわりの Taylor 展開
の 0
のまわりの Taylor 展開
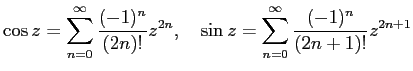
![]()
![]() の 0
のまわりの Taylor 展開を
の 0
のまわりの Taylor 展開を ![]() 次の項まで求めよ。
次の項まで求めよ。
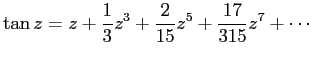
を掲げておく。