A..1.1.3 頑張って星形の$10$ 個の頂点を計算する

紙の上に星形を (ある程度正確に) 描いて、 頂点の座標を求めましょう。 頂点は「外側の円周上にあるもの」と「内側の円周上にあるもの」の 二種類あり、 それぞれ正五角形の頂点をなすことは容易に分かります。

半径$1$ の円に内接する星形とすると、 外側の円周上にある頂点 $(x_j,y_j)$ ( $j=1,2,3,4,5$ ) は、 上で提示した式で計算出来ることになります。

内側の円周上にある頂点 $(\overline x_j,\overline y_j)$ ( $j=1,2,3,4,5$ ) は (適当に番号を振ります)、 次の性質を持つことは明らかです。

(1)

ある正数 $r$ ($0<r<1$ ) を半径とする原点中心の円周上にある。

(2)

$(\overline x_j,\overline y_j)$ の角度は、 $(x_j,y_j)$ の角度と $(x_{j+1},y_{j+1})$ の角度のちょうど真ん中 (ただし $(x_{6},y_{6})=(x_1,y_1)$ とする)。

$r$ さえ求まれば、後は正五角形を描くのとほとんど同様の計算です。 とりあえず $r$ はユーザーに入力してもらうことにすると、 次のようなプログラムが書けます。

kadai6b4.BAS

REM kadai6b4.BAS --- 星を描く（後一歩バージョン）
OPTION ANGLE DEGREES
SET WINDOW -1,1,-1,1
DIM X(10),Y(10)
INPUT PROMPT "内側の円の半径 r": r
LET DT=360/10
FOR j=1 TO 10
   LET T=(j-1)*DT+90
   REM j が奇数か偶数かで場合分け
   IF MOD(j,2)=1 THEN
      LET x(j)=COS(t)
      LET y(j)=SIN(t)
   ELSE
      LET x(j)=r*COS(t)
      LET y(j)=r*SIN(t)
   END IF
NEXT j
SET AREA COLOR "red"
MAT PLOT AREA : x,y 
END

$r$ ($<1$ ) の値を色々変えて試してみましょう。 $r=0.4$ くらいが良さそうです。

正確な星形を与える $r$ は、図形の相似比を考えたりして求められます。 詳細は自分で解きたい人のお楽しみで取っておきますが (あしからず)、 結果は

$$r=\frac{\sin 18^\circ}{\cos 36^\circ} =\frac{\cos 72^\circ}{\cos... ...+1)/4} =\frac{\sqrt{5}-1}{\sqrt{5}+1} =\frac{3-\sqrt{5}}{2}=0.38196601\cdots$$

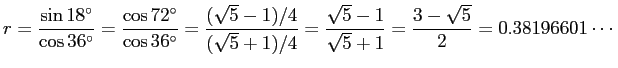
です。

kadai6b4.BAS の

INPUT PROMPT "内側の円の半径 r": r

を

LET r=(SQR(5)-1)/(SQR(5)+1)

に変えると、図 6 のようにきれいな星が描けます。

図 6: 完成版