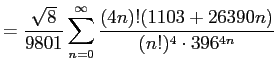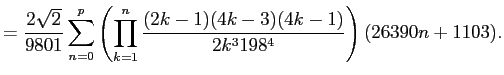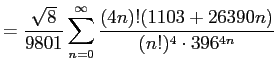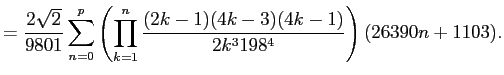

Next: A..2.4.2 DRM の発見
Up: A..2.4 現在の到達点
Previous: A..2.4 現在の到達点
不思議な天才 Ramanujan (Srinivasa Aiyangar Ramanujan, 1887-1920,
インドの Erode に生まれ、インドの Kumbakonam にて没する) が発見した
や、その系統の公式がいくつかあります。
Chudnovsky の公式 (現在最高速?)

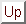

Next: A..2.4.2 DRM の発見
Up: A..2.4 現在の到達点
Previous: A..2.4 現在の到達点
桂田 祐史
2013-06-12