![\includegraphics[width=10cm]{eps/problem6.eps}](img306.png)
|
In[1] := g[x_,y_]:=x^2+2x y+3y^2-4
In[2] := Ng=ContourPlot[g[x,y]==0,{x,-3,3},{y,-3,3},ContourStyle->Green]
|
![]() on
on ![]() が分かるので (省略する)、
極値点は Lagrange の未定乗数法で見つかるはずである。
そこで未定乗数法で極値点の候補を求め、それらの点における
が分かるので (省略する)、
極値点は Lagrange の未定乗数法で見つかるはずである。
そこで未定乗数法で極値点の候補を求め、それらの点における ![]() の値を計算する。
の値を計算する。
In[3] := f[x_,y_]:=x^2+y^2
In[4] := s=Solve[{D[f[x,y]-L g[x,y],{{x,y}}]=={0,0}, g[x,y]==0},{x,y,L}]
In[5] := f[x,y]/.s
|
![]() ,
, ![]() の解は
の解は
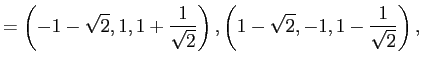 |
||
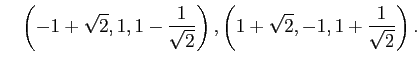 |
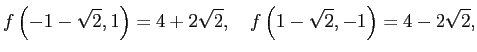 |
||
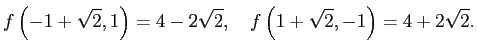 |
In[6] := fc=ContourPlot[f[x,y],{x,-3,3},{y,-3,3},
ContourShading->False,ContourStyle->Blue,
Contours->Table[4+2Sqrt[2]/4*i,{i,-8,8}]]
In[7] := sp = ListPlot[{x,y} /. s, PlotStyle->Red]
In[8] := gr=Show[fc,Ng,sp]
|